Introduction to Generic Trees (N-ary Trees)

Generic trees are a collection of nodes where each node is a data structure that consists of records and a list of references to its children(duplicate references are not allowed). Unlike the linked list, each node stores the address of multiple nodes. Every node stores address of its children and the very first node’s address will be stored in a separate pointer called root.

The Generic trees are the N-ary trees which have the following properties: 

            1. Many children at every node.

            2. The number of nodes for each node is not known in advance.

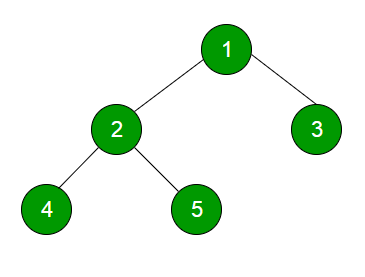
Example: 
 

Generic Tree

To represent the above tree, we have to consider the worst case, that is the node with maximum children (in above example, 6 children) and allocate that many pointers for each node.
The node representation based on this method can be written as:
 

C++

| // Node declaration struct Node{ int data; Node *firstchild; Node *secondchild; Node *thirdchild; Node *fourthchild; Node *fifthchild; Node *sixthchild; }; | | — |

C

| //Node declaration struct Node{ int data; struct Node *firstchild; struct Node *secondchild; struct Node *thirdchild; struct Node *fourthchild; struct Node *fifthchild; struct Node *sixthchild; } | | — |

Java

| // Java code for above approach public class Node { int data; Node firstchild; Node secondchild; Node thirdchild; Node fourthchild; Node fifthchild; Node sixthchild; } | | — |

Python

| class Node: def __init__(self, data): self.data = data self.firstchild = None self.secondchild = None self.thirdchild = None self.fourthchild = None self.fifthchild = None self.sixthchild = None | | — |

C#

| public class Node { public int Data { get; set; } public Node Firstchild { get; set; } public Node Secondchild { get; set; } public Node Thirdchild { get; set; } public Node Fourthchild { get; set; } public Node Fifthchild { get; set; } public Node Sixthchild { get; set; } } | | — |

Javascript

| // Javascript code for above approach class Node { constructor(data) { this.data = data; this.firstchild = null; this.secondchild = null; this.thirdchild = null; this.fourthchild = null; this.fifthchild = null; this.sixthchild = null; } } | | — |

Disadvantages of the above representation are: 

1. Memory Wastage – All the pointers are not required in all the cases. Hence, there is lot of memory wastage.
2. Unknown number of children – The number of children for each node is not known in advance.

Simple Approach: 

For storing the address of children in a node we can use an array or linked list. But we will face some issues with both of them.

1. In Linked list, we can not randomly access any child’s address. So it will be expensive.
2. In array, we can randomly access the address of any child, but we can store only fixed number of children’s addresses in it.

Better Approach:

We can use Dynamic Arrays for storing the address of children. We can randomly access any child’s address and the size of the vector is also not fixed.

C++

| #include <vector>   class Node { public: int data; std::vector<Node*> children;   Node(int data) { this->data = data; } }; | | — |

C

| //Node declaration struct Node{ int data; vector<Node*> children; } | | — |

Java

| import java.util.ArrayList;   class Node { int data; ArrayList<Node> children;   Node(int data) { this.data = data; this.children = new ArrayList<Node>(); } } | | — |

Python

| class Node:   def __init__(self,data): self.data=data self.children=[] | | — |

C#

| using System.Collections.Generic;   class Node { public int data; public List<Node> children;   public Node(int data) { this.data = data; this.children = new List<Node>(); } }   // This code is contributed by adityamaharshi21. | | — |

Javascript

| class Node { constructor(data) { this.data = data; this.children = []; } } | | — |

Efficient Approach:

First child / Next sibling representation

 In the first child/next sibling representation, the steps taken are: 

At each node-link the children of the same parent(siblings) from left to right.

• Remove the links from parent to all children except the first child.

Since we have a link between children, we do not need extra links from parents to all the children. This representation allows us to traverse all the elements by starting at the first child of the parent.
 

FIRST CHILD/NEXT SIBLING REPRESENTATION

The node declaration for first child / next sibling representation can be written as: 
 

C++

| struct Node { int data; Node *firstChild; Node *nextSibling; }; | | — |

C

| //Node declaration struct Node{ int data; struct Node *firstChild; struct Node *nextSibling; } | | — |

Java

| class Node { int data; Node firstChild; Node nextSibling; } | | — |

Python

| class Node: def __init__(self, data): self.data = data self.firstChild = None self.nextSibling = None   # This code is contributed by aadityamaharshi | | — |

Javascript

| class Node { constructor(data) { this.data = data; this.firstChild = null; this.nextSibling = null; } } | | — |

C#

| public class Node { public int Data { get; set; } public Node FirstChild { get; set; } public Node NextSibling { get; set; } } | | — |

Advantages: 

• Memory efficient – No extra links are required, hence a lot of memory is saved.
• Treated as binary trees – Since we are able to convert any generic tree to binary representation, we can treat all generic trees with a first child/next sibling representation as binary trees. Instead of left and right pointers, we just use firstChild and nextSibling.
• Many algorithms can be expressed more easily because it is just a binary tree.
• Each node is of fixed size ,so no auxiliary array or vector is required.

Height of generic tree from parent array 
Generic tree – level order traversal

Next

What is Generic Tree or N-ary Tree

---

Introduction to Binary Tree – Data Structure and Algorithm Tutorials ====================================================================

**Binary Tree** is a **non-linear data structure** where each node has at most two children. In this article, we will cover all the basics of Binary Tree, Operations on Binary Tree, its implementation, advantages, disadvantages which will help you solve all the problems based on Binary Tree.

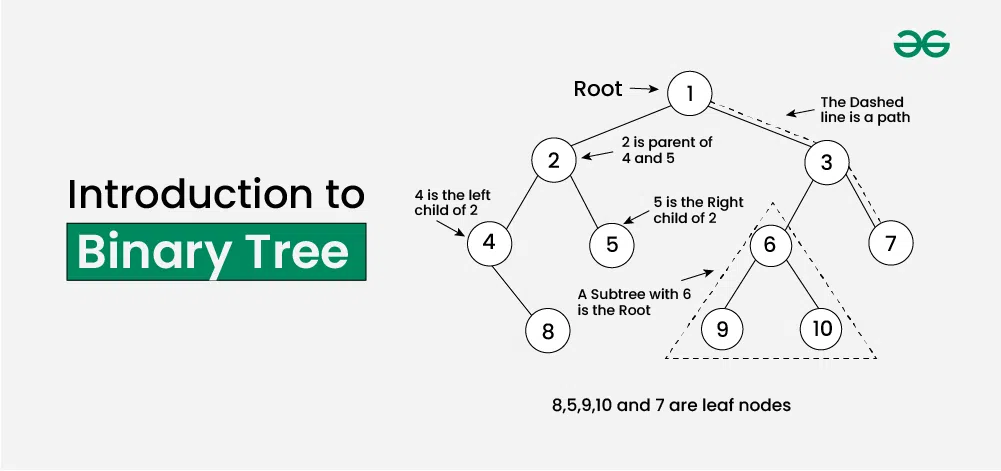
Table of Content

• What is Binary Tree?
• Representation of Binary Tree
• Types of Binary Tree
• Operations On Binary Tree
  • Insertion in Binary Tree
  • Traversal of Binary Tree
  • Deletion in Binary Tree
  • Searching in Binary Tree
• Auxiliary Operations On Binary Tree
• Implementation of Binary Tree
• Complexity Analysis of Binary Tree Operations
• Advantages of Binary Tree
• Disadvantages of Binary Tree
• Applications of Binary Tree
• Frequently Asked Questions on Binary Tree What is Binary Tree? ——————–

Binary tree is a **tree data structure(non-linear)** in which each node can have **at most two children** which are referred to as the **left child** and the **right child**. 

The topmost node in a binary tree is called the **root, and the bottom-most nodes are called **leaves**. A binary tree can be visualized as a hierarchical structure with the root at the top and the leaves at the bottom.

**Representation of Binary Tree**

Each node in a Binary Tree has three parts:

• Data
• Pointer to the left child
• Pointer to the right child

Below is the representation of a Node of Binary Tree in different languages:

// Use any below method to implement Nodes of tree

// Method 1: Using "struct" to make
// user-define data type
struct node {
    int data;
    struct node* left;
    struct node* right;
};

// Method 2: Using "class" to make
// user-define data type
class Node {
public:
    int data;
    Node* left;
    Node* right;
};

// Class containing left and right child
// of current node and key value
class Node {
    int key;
    Node left, right;

    public Node(int item)
    {
        key = item;
        left = right = null;
    }
}

Types of Binary Tree

Binary Tree can be classified into multiples types based on multiple factors:

• **On the basis of Number of Children**
  • Full Binary Tree
  • Degenerate Binary Tree
  • Skewed Binary Trees
• **On the basis of Completion of Levels**
  • Complete Binary Tree
  • Perfect Binary Tree
  • Balanced Binary Tree
• **On the basis of Node Values:**
  • Binary Search Tree
  • AVL Tree
  • Red Black Tree
  • B Tree
  • B+ Tree
  • Segment Tree

**Operations On Binary Tree**

1. Insertion in Binary Tree

We can insert a node anywhere in a binary tree by inserting the node as the left or right child of any node or by making the node as root of the tree.

**Algorithm to insert a node in a Binary Tree:**

• Check if there is a node in the binary tree, which has missing left child. If such a node exists, then insert the new node as its left child.
• Check if there is a node in the binary tree, which has missing right child. If such a node exists, then insert the new node as its right child.
• If we don’t find any node with missing left or right child, then find the node which has both the children missing and insert the node as its left or right child.

1. Traversal of Binary Tree

Traversal of Binary Tree involves visiting all the nodes of the binary tree. Tree Traversal algorithms can be classified broadly into two categories:

• Depth-First Search (DFS) Algorithms
• Breadth-First Search (BFS) Algorithms

Depth-First Search (DFS) algorithms:

• **Preorder Traversal (current-left-right):** Visit the current node before visiting any nodes inside the left or right subtrees. Here, the traversal is root – left child – right child. It means that the root node is traversed first then its left child and finally the right child.
• **Inorder Traversal (left-current-right):**Visit the current node after visiting all nodes inside the left subtree but before visiting any node within the right subtree. Here, the traversal is left child – root – right child.  It means that the left child is traversed first then its root node and finally the right child.
• **Postorder Traversal (left-right-current):** Visit the current node after visiting all the nodes of the left and right subtrees. Here, the traversal is left child – right child – root.  It means that the left child has traversed first then the right child and finally its root node.

Breadth-First Search (BFS) algorithms:

• **Level Order Traversal:** Visit nodes level-by-level and left-to-right fashion at the same level. Here, the traversal is level-wise. It means that the most left child has traversed first and then the other children of the same level from left to right have traversed.

1. Deletion in Binary Tree

We can delete any node in the binary tree and rearrange the nodes after deletion to again form a valid binary tree.

**Algorithm to delete a node in a Binary Tree:**

• Starting at the root, find the deepest and rightmost node in the binary tree and the node which we want to delete.
• Replace the deepest rightmost node’s data with the node to be deleted.
• Then delete the deepest rightmost node.

1. Searching in Binary Tree

We can search for an element in the node by using any of the traversal techniques.

**Algorithm to search a node in a Binary Tree:**

• Start from the root node.
• Check if the current node’s value is equal to the target value.
• If the current node’s value is equal to the target value, then this node is the required node.
• Otherwise, if the node’s value is not equal to the target value, start the search in the left and right child.
• If we do not find any node whose value is equal to target, then the value is not present in the tree.

**Auxiliary Operations On Binary Tree**

• Finding the height of the tree
• Find level of a node in a Binary tree
• Finding the size of the entire tree

Implementation of Binary Tree

Below is the code for insertion, deletion and traversal of the binary tree:

import java.util.LinkedList;
import java.util.Queue;

// Node class to define the structure of the node
class Node {
    int data;
    Node left, right;
    // Parameterized Constructor
    Node(int val) {
        data = val;
        left = right = null;
    }
}

public class BinaryTree {
    // Function to insert nodes
    public static Node insert(Node root, int data) {
        // If tree is empty, new node becomes the root
        if (root == null) {
            root = new Node(data);
            return root;
        }
        // Queue to traverse the tree and find the position to
        // insert the node
        Queue<Node> q = new LinkedList<>();
        q.offer(root);
        while (!q.isEmpty()) {
            Node temp = q.poll();
            // Insert node as the left child of the parent node
            if (temp.left == null) {
                temp.left = new Node(data);
                break;
            }
            // If the left child is not null push it to the
            // queue
            else
                q.offer(temp.left);
            // Insert node as the right child of parent node
            if (temp.right == null) {
                temp.right = new Node(data);
                break;
            }
            // If the right child is not null push it to the
            // queue
            else
                q.offer(temp.right);
        }
        return root;
    }

    /* function to delete the given deepest node
    (d_node) in binary tree */
    public static void deletDeepest(Node root, Node d_node) {
        Queue<Node> q = new LinkedList<>();
        q.offer(root);
        // Do level order traversal until last node
        Node temp;
        while (!q.isEmpty()) {
            temp = q.poll();
            if (temp == d_node) {
                temp = null;
                d_node = null;
                return;
            }
            if (temp.right != null) {
                if (temp.right == d_node) {
                    temp.right = null;
                    d_node = null;
                    return;
                } else
                    q.offer(temp.right);
            }
            if (temp.left != null) {
                if (temp.left == d_node) {
                    temp.left = null;
                    d_node = null;
                    return;
                } else
                    q.offer(temp.left);
            }
        }
    }

    /* function to delete element in binary tree */
    public static Node deletion(Node root, int key) {
        if (root == null)
            return null;
        if (root.left == null && root.right == null) {
            if (root.data == key)
                return null;
            else
                return root;
        }
        Queue<Node> q = new LinkedList<>();
        q.offer(root);
        Node temp = new Node(0);
        Node key_node = null;
        // Do level order traversal to find deepest
        // node(temp) and node to be deleted (key_node)
        while (!q.isEmpty()) {
            temp = q.poll();
            if (temp.data == key)
                key_node = temp;
            if (temp.left != null)
                q.offer(temp.left);
            if (temp.right != null)
                q.offer(temp.right);
        }
        if (key_node != null) {
            int x = temp.data;
            key_node.data = x;
            deletDeepest(root, temp);
        }
        return root;
    }

    // Inorder tree traversal (Left - Root - Right)
    public static void inorderTraversal(Node root) {
        if (root == null)
            return;
        inorderTraversal(root.left);
        System.out.print(root.data + " ");
        inorderTraversal(root.right);
    }

    // Preorder tree traversal (Root - Left - Right)
    public static void preorderTraversal(Node root) {
        if (root == null)
            return;
        System.out.print(root.data + " ");
        preorderTraversal(root.left);
        preorderTraversal(root.right);
    }

    // Postorder tree traversal (Left - Right - Root)
    public static void postorderTraversal(Node root) {
        if (root == null)
            return;
        postorderTraversal(root.left);
        postorderTraversal(root.right);
        System.out.print(root.data + " ");
    }

    // Function for Level order tree traversal
    public static void levelorderTraversal(Node root) {
        if (root == null)
            return;

        // Queue for level order traversal
        Queue<Node> q = new LinkedList<>();
        q.offer(root);
        while (!q.isEmpty()) {
            Node temp = q.poll();
            System.out.print(temp.data + " ");
            // Push left child in the queue
            if (temp.left != null)
                q.offer(temp.left);
            // Push right child in the queue
            if (temp.right != null)
                q.offer(temp.right);
        }
    }

    /* Driver function to check the above algorithm. */
    public static void main(String[] args) {
        Node root = null;
        // Insertion of nodes
        root = insert(root, 10);
        root = insert(root, 20);
        root = insert(root, 30);
        root = insert(root, 40);

        System.out.print("Preorder traversal: ");
        preorderTraversal(root);

        System.out.print("\nInorder traversal: ");
        inorderTraversal(root);

        System.out.print("\nPostorder traversal: ");
        postorderTraversal(root);

        System.out.print("\nLevel order traversal: ");
        levelorderTraversal(root);

        // Delete the node with data = 20
        root = deletion(root, 20);

        System.out.print("\nInorder traversal after deletion: ");
        inorderTraversal(root);
    }
}

#include <bits/stdc++.h>
using namespace std;

// Node class to define the structure of the node
class Node {
public:
    int data;
    Node *left, *right;
    // Parameterized Constructor
    Node(int val)
    {
        data = val;
        left = right = NULL;
    }
};

// Function to insert nodes
Node* insert(Node* root, int data)
{
    // If tree is empty, new node becomes the root
    if (root == NULL) {
        root = new Node(data);
        return root;
    }
    // queue to traverse the tree and find the position to
    // insert the node
    queue<Node*> q;
    q.push(root);
    while (!q.empty()) {
        Node* temp = q.front();
        q.pop();
        // Insert node as the left child of the parent node
        if (temp->left == NULL) {
            temp->left = new Node(data);
            break;
        }
        // If the left child is not null push it to the
        // queue
        else
            q.push(temp->left);
        // Insert node as the right child of parent node
        if (temp->right == NULL) {
            temp->right = new Node(data);
            break;
        }
        // If the right child is not null push it to the
        // queue
        else
            q.push(temp->right);
    }
    return root;
}

/* function to delete the given deepest node
(d_node) in binary tree */
void deletDeepest(Node* root, Node* d_node)
{
    queue<Node*> q;
    q.push(root);
    // Do level order traversal until last node
    Node* temp;
    while (!q.empty()) {
        temp = q.front();
        q.pop();
        if (temp == d_node) {
            temp = NULL;
            delete (d_node);
            return;
        }
        if (temp->right) {
            if (temp->right == d_node) {
                temp->right = NULL;
                delete (d_node);
                return;
            }
            else
                q.push(temp->right);
        }
        if (temp->left) {
            if (temp->left == d_node) {
                temp->left = NULL;
                delete (d_node);
                return;
            }
            else
                q.push(temp->left);
        }
    }
}

/* function to delete element in binary tree */
Node* deletion(Node* root, int key)
{
    if (!root)
        return NULL;
    if (root->left == NULL && root->right == NULL) {
        if (root->data == key)
            return NULL;
        else
            return root;
    }
    queue<Node*> q;
    q.push(root);
    Node* temp;
    Node* key_node = NULL;
    // Do level order traversal to find deepest
    // node(temp) and node to be deleted (key_node)
    while (!q.empty()) {
        temp = q.front();
        q.pop();
        if (temp->data == key)
            key_node = temp;
        if (temp->left)
            q.push(temp->left);
        if (temp->right)
            q.push(temp->right);
    }
    if (key_node != NULL) {
        int x = temp->data;
        key_node->data = x;
        deletDeepest(root, temp);
    }
    return root;
}

// Inorder tree traversal (Left - Root - Right)
void inorderTraversal(Node* root)
{
    if (!root)
        return;
    inorderTraversal(root->left);
    cout << root->data << " ";
    inorderTraversal(root->right);
}

// Preorder tree traversal (Root - Left - Right)
void preorderTraversal(Node* root)
{
    if (!root)
        return;
    cout << root->data << " ";
    preorderTraversal(root->left);
    preorderTraversal(root->right);
}

// Postorder tree traversal (Left - Right - Root)
void postorderTraversal(Node* root)
{
    if (root == NULL)
        return;
    postorderTraversal(root->left);
    postorderTraversal(root->right);
    cout << root->data << " ";
}

// Function for Level order tree traversal
void levelorderTraversal(Node* root)
{
    if (root == NULL)
        return;

    // Queue for level order traversal
    queue<Node*> q;
    q.push(root);
    while (!q.empty()) {
        Node* temp = q.front();
        q.pop();
        cout << temp->data << " ";
        // Push left child in the queue
        if (temp->left)
            q.push(temp->left);
        // Push right child in the queue
        if (temp->right)
            q.push(temp->right);
    }
}

/* Driver function to check the above algorithm. */
int main()
{
    Node* root = NULL;
    // Insertion of nodes
    root = insert(root, 10);
    root = insert(root, 20);
    root = insert(root, 30);
    root = insert(root, 40);

    cout << "Preorder traversal: ";
    preorderTraversal(root);

    cout << "\nInorder traversal: ";
    inorderTraversal(root);

    cout << "\nPostorder traversal: ";
    postorderTraversal(root);

    cout << "\nLevel order traversal: ";
    levelorderTraversal(root);

    // Delete the node with data = 20
    root = deletion(root, 20);

    cout << "\nInorder traversal after deletion: ";
    inorderTraversal(root);
}

Output

Preorder traversal: 10 20 40 30 
Inorder traversal: 40 20 10 30 
Postorder traversal: 40 20 30 10 
Level order traversal: 10 20 30 40 
Inorder traversal after deletion: 40 10 30 

Complexity Analysis of Binary Tree Operations ———————————————

**Operations**	**Time Complexity**	**Space Complexity**
**Insertion**	O(N)	O(N)
**Preorder Traversal**	O(N)	O(N)
Inorder Traversal	O(N)	O(N)
Postorder Traversal	O(N)	O(N)
Level Order Traversal	O(N)	O(N)
Deletion	O(N)	O(N)
Searching	O(N)	O(N)

We can use **Morris Traversal**to traverse all the nodes of the binary tree in O(1) time.

Advantages of Binary Tree

• **Efficient Search:** Binary trees are efficient when searching for a specific element, as each node has at most two child nodes, allowing for **binary search** algorithms to be used.
• **Memory Efficient:** Binary trees require lesser memory as compared to other tree data structures, therefore they are memory-efficient.
• Binary trees are relatively easy to implement and understand as each node has at most two children, left child and right child.

Disadvantages of Binary Tree

• **Limited structure:**Binary trees are limited to two child nodes per node, which can limit their usefulness in certain applications. For example, if a tree requires more than two child nodes per node, a different tree structure may be more suitable.
• **Unbalanced trees:**Unbalanced binary trees, where one subtree is significantly larger than the other, can lead to inefficient search operations. This can occur if the tree is not properly balanced or if data is inserted in a non-random order.
• **Space inefficiency:**Binary trees can be space inefficient when compared to other data structures. This is because each node requires two child pointers, which can be a significant amount of memory overhead for large trees.
• **Slow performance in worst-case scenarios:** In the worst-case scenario, a binary tree can become degenerate or skewed, meaning that each node has only one child. In this case, search operations can degrade to O(n) time complexity, where n is the number of nodes in the tree.

**Applications of Binary Tree**

• Binary Tree can be used to **represent hierarchical data**.
• Huffman Coding trees are used in **data compression algorithms**.
• Priority Queue is another application of binary tree that is used for searching maximum or minimum in O(1) time complexity.
• Useful for indexing segmented at the database is useful in storing cache in the system,
• Binary trees can be used to implement decision trees, a type of machine learning algorithm used for classification and regression analysis.

Frequently Asked Questions on Binary Tree

1. What is a binary tree?

A binary tree is a non-linear data structure consisting of nodes, where each node has at most two children (left child and the right child).

2. What are the types of binary trees?

Binary trees can be classified into various types, including full binary trees, complete binary trees, perfect binary trees, balanced binary trees (such as AVL trees and Red-Black trees), and degenerate (or pathological) binary trees.

3. What is the height of a binary tree?

The height of a binary tree is the length of the longest path from the root node to a leaf node. It represents the number of edges in the longest path from the root node to a leaf node.

4. What is the depth of a node in a binary tree?

The depth of a node in a binary tree is the length of the path from the root node to that particular node. The depth of the root node is 0.

5. How do you perform tree traversal in a binary tree?

Tree traversal in a binary tree can be done in different ways: In-order traversal, Pre-order traversal, Post-order traversal, and Level-order traversal (also known as breadth-first traversal).

6. What is an Inorder traversal in Binary Tree?

In Inorder traversal, nodes are recursively visited in this order: left child, root, right child. This traversal results in nodes being visited in non-decreasing order in a binary search tree.

7. What is a Preorder traversal in Binary Tree?

In Preorder traversal, nodes are recursively visited in this order: root, left child, right child. This traversal results in root node being the first node to be visited.

8. What is a Postorder traversal in Binary Tree?

In Postorder traversal, nodes are recursively visited in this order: left child, right child and root. This traversal results in root node being the last node to be visited.

9. What is the difference between a Binary Tree and a Binary Search Tree?

A binary tree is a hierarchical data structure where each node has at most two children, whereas a binary search tree is a type of binary tree in which the left child of a node contains values less than the node’s value, and the right child contains values greater than the node’s value.

**10. What is a balanced binary tree?**

A balanced binary tree is a binary tree in which the height of the left and right subtrees of every node differ by at most one. Balanced trees help maintain efficient operations such as searching, insertion, and deletion with time complexities close to O(log n).

Conclusion:

Tree is a hierarchical data structure. Main uses of trees include maintaining hierarchical data, providing moderate access and insert/delete operations. Binary trees are special cases of tree where every node has at most two children.

Related Articles:

• Properties of Binary Tree
• Types of Binary Tree

Previous

Binary Tree Data Structure

Next

Properties of Binary Tree

---

Complete Binary Tree ====================

We know a **tree** is a non-linear data structure. It has no limitation on the number of children. A binary tree has a limitation as any node of the tree has at most two children: a left and a right child.

**What is a Complete Binary Tree?**

A complete binary tree is a special type of binary tree where all the levels of the tree are filled completely except the lowest level nodes which are filled from as left as possible.

Complete Binary Tree

**Some terminology of Complete Binary Tree:**

• **Root** – Node in which no edge is coming from the parent. Example -node A
• **Child** – Node having some incoming edge is called child. Example – nodes B, F are the child of A and C respectively.
• **Sibling** – Nodes having the same parent are sibling. Example- D, E are siblings as they have the same parent B.
• **Degree of a node** – Number of children of a particular parent. Example- Degree of A is 2 and Degree of C is 1. Degree of D is 0.
• **Internal/External nodes** – Leaf nodes are external nodes and non leaf nodes are internal nodes.
• **Level** – Count nodes in a path to reach a destination node. Example- Level of node D is 2 as nodes A and B form the path.
• **Height** – Number of edges to reach the destination node, Root is at height 0. Example – Height of node E is 2 as it has two edges from the root.

**Properties of Complete Binary Tree:**

• A complete binary tree is said to be a proper binary tree where all leaves have the same depth.
• In a complete binary tree number of nodes at depth **d** is **2**d**.
• In a  complete binary tree with **n** nodes height of the tree is **log(n+1)**.
• All the levels **except the last level** are completely full.

[**Perfect Binary Tree](https://www.geeksforgeeks.org/check-weather-given-binary-tree-perfect-not/) **vs Complete Binary Tree:**

A binary tree of height ‘h’ having the maximum number of nodes is a **perfect** binary tree. 
For a given height **h, the maximum number of nodes is **2**h+1**-1**.

A **complete** binary tree of height h is a perfect binary tree up to height **h-1**, and in the last level element are stored in left to right order.

**Example 1:**

A Binary Tree

The height of the given binary tree is 2 and the maximum number of nodes in that tree is n= 2h+1-1 =  22+1-1 =  23-1 = **7.
Hence we can conclude it is **a perfect binary tree**.
Now for a complete binary tree, It is full up to height **h-1** i.e.; 1, and the last level elements are stored in left to right order. Hence it is a complete Binary tree also. Here is the representation of elements when stored in an array

Element stored in an array level by level

In the array, all the elements are stored continuously.

**Example 2:**

A binary tree

Height of the given binary tree is 2 and the maximum number of nodes that should be there are 2h+1 – 1 = 22+1 – 1 = 23 – 1 = **7. 
But the number of nodes in the tree is **6**. Hence it is **not a perfect binary tree**.
Now for a complete binary tree, It is full up to height **h-1** i.e.; **1**, and the last level element are stored in left to right order. Hence this is a **complete binary tree**. Store the element in an array and it will be like;

Element stored in an array level by level

**Example 3:**

A binary tree

The height of the binary tree is 2 and the maximum number of nodes that can be there is 7, but there are only 5 nodes hence it is **not a perfect binary tree.
In case of a complete binary tree, we see that in the last level elements are not filled from left to right order. So it is **not a complete binary tree**.

Element stored in an array level by level

The elements in the array are not continuous.

**Full Binary Tree vs Complete Binary tree:**

For a full binary tree, every node has either 2 children or 0 children.

**Example 1:**

A binary tree

In the given binary tree there is no node having degree 1, either 2 or 0 children for every node, hence it is **a full binary tree**.

For a complete binary tree, elements are stored in level by level and not from the leftmost side in the last level. Hence this is **not a complete binary tree**. The array representation is:

Element stored in an array level by level

**Example 2:**

A binary Tree

In the given binary tree there is no node having degree 1. Every node has a degree of either 2 or 0. Hence it is a **full binary tree**.

For a complete binary tree, elements are stored in a level by level manner and filled from the leftmost side of the last level. Hence this a **complete binary tree**. Below is the array representation of the tree:

Element stored in an array level by level

**Example 3:**

A binary tree

In the given binary tree node B has degree 1 which violates the property of full binary tree hence it is **not a full Binary tree**

For a complete binary tree, elements are stored in level by level manner and filled from the leftmost side of the last level. Hence this is a **complete binary tree**. Array representation of the binary tree is:

Element stored in an array level by level

**Example 4:**
 

a binary tree

In the given binary tree node C has degree 1 which violates the property of a full binary tree hence it is **not a full Binary tree**

For a complete binary tree, elements are stored in level by level manner and filled from the leftmost side of the last level. Here node E violates the condition. Hence this is **not a complete binary tree**. 

**Creation of Complete Binary Tree:**

We know a **complete binary tree** is a tree in which except for the last level (say **l)all the other level has (2l) nodes and the nodes are lined up from left to right side.
It can be represented using an array. If the parent is it index **i** so the left child is at **2i+1** and the right child is at **2i+2**.

Complete binary tree and its array representation

**Algorithm:**

For the creation of a **Complete Binary Tree**, we require a queue data structure to keep track of the inserted nodes.

**Step 1:** Initialize the root with a new node when the tree is empty.

**Step 2:** If the tree is not empty then get the front element 

• If the front element does not have a left child then set the left child to a new node
• If the right child is not present set the right child as a new node

**Step 3:** If the node has both the children then **pop** it from the queue.

**Step 4:** Enqueue the new data.

**Illustration:**

Consider the below array:

1. The 1st element will the root (value at index = **0**)

A is taken as root

1. The next element (at index = **1) will be left and third element (index = **2**) will be right child of root

B as left child and D as right child

1. fourth (index = **3) and fifth element (index = **4**) will be the left and right child of B node

E and F are left and right child of B

1. Next element (index = **5**) will be left child of the node D

G is made left child of D node

This is how complete binary tree is created.

**Implementation:** For the implementation of building a Complete Binary Tree from level order traversal is given in **this post**.

**Application of the Complete binary tree:**

• Heap Sort
• Heap sort-based data structure

**Check if a given binary tree is complete or not:** Follow **this post** to check if the given binary tree is complete or not.

Previous

Types of Binary Tree

Next

Perfect Binary Tree

---

Perfect Binary Tree ===================

What is a Perfect Binary Tree?

A perfect binary tree is a special type of binary tree in which all the leaf nodes are at the same depth, and all non-leaf nodes have two children. In simple terms, this means that all leaf nodes are at the maximum depth of the tree, and the tree is completely filled with no gaps.

The maximum number of nodes in a perfect binary tree is given by the formula 2^(d+1) – 1, where d is the depth of the tree. This means that a perfect binary tree with a depth of n has 2^n leaf nodes and a total of 2^(n+1) – 1 nodes.

Perfect binary trees have a number of useful properties that make them useful in various applications. For example, they are often used in the implementation of heap data structures, as well as in the construction of threaded binary trees. They are also used in the implementation of algorithms such as heapsort and merge sort.

In other words, it can be said that each level of the tree is completely filled by the nodes.

Examples of Perfect Binary Tree:

Example of a Perfect Binary Tree

A tree with only the root node is also a perfect binary tree.     

Example-2

The following tree is not a perfect binary tree because the last level of the tree is not completely filled.

Not a Perfect Binary Tree

Properties of a Perfect Binary Tree:

• Degree: The degree of a node of a tree is defined as the number of children of that node. All the internal nodes have a degree of 2. The leaf nodes of a perfect binary tree have a degree of 0.
• Number of leaf nodes: If the height of the perfect binary tree is h, then the number of leaf nodes will be 2h because the last level is completely filled.
• Depth of a node: Average depth of a node in a perfect binary tree is Θ(ln(n)).
• Relation between leaf nodes and non-leaf nodes: No. of leaf nodes = No. of non-leaf nodes +1.
• Total number of nodes: A tree of height h has total nodes = 2h+1 – 1. Each node of the tree is filled. So total number of nodes can be calculated as 20 + 21 + . . . + 2h = 2h+1 – 1.
• Height of the tree: The height of a perfect binary tree with N number of nodes = log(N + 1) – 1 = Θ(ln(n)). This can be calculated using the relation shown while calculating the total number of nodes in a perfect binary tree.

Check whether a tree is a Perfect Binary Tree or not:

• Check the depth of the tree. A perfect binary tree is defined as a tree where all leaf nodes are at the same depth, and all non-leaf nodes have two children. To check whether a tree is a perfect binary tree, you can first calculate the depth of the tree.
• Check the number of nodes at each level: Once you have calculated the depth of the tree, you can then check the number of nodes at each level. In a perfect binary tree, the number of nodes at each level should be a power of 2 (e.g. 1, 2, 4, 8, etc.). If any level has a different number of nodes, the tree is not a perfect binary tree.

For more information about this refer to the article article: Check whether a given binary tree is perfect or not

Summary:

• All leaf nodes are at the same depth. In a perfect binary tree, all leaf nodes are at the maximum depth of the tree. This means that the tree is completely filled with no gaps.
• All non-leaf nodes have two children. In a perfect binary tree, all non-leaf nodes have exactly two children. This means that the tree has a regular structure, with all nodes having either two children or no children.
• The maximum number of nodes is given by a formula: The maximum number of nodes in a perfect binary tree is given by the formula 2^(d+1) – 1, where d is the depth of the tree.
• They have a symmetrical structure. This is because all non-leaf nodes have two children, perfect binary trees have a symmetrical structure.
• They can be represented using an array. Perfect binary trees can be represented using an array, where the left child of a node at index i is stored at index 2i+1 and the right child is stored at index 2i+2. This makes it easy to access the children of a node and to traverse the tree.

Previous

Complete Binary Tree

Next

Level Order Traversal (Breadth First Search or BFS) of Binary Tree

---

Balanced Binary Tree ====================

A binary tree is balanced if the height of the tree is O(Log n) where n is the number of nodes. For Example, the AVL tree maintains O(Log n) height by making sure that the difference between the heights of the left and right subtrees is at most 1. Red-Black trees maintain O(Log n) height by making sure that the number of Black nodes on every root-to-leaf path is the same and that there are no adjacent red nodes. Balanced Binary Search trees are performance-wise good as they provide O(log n) time for search, insert and delete. 

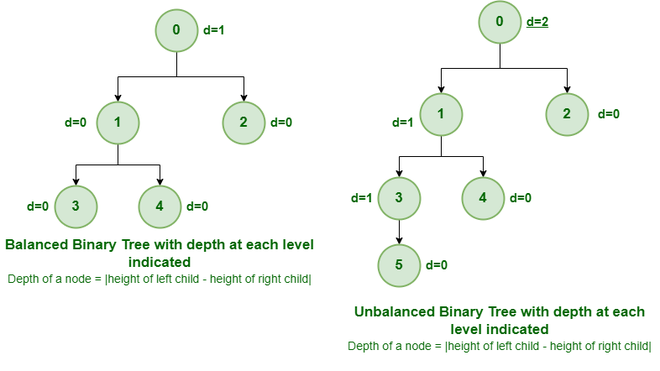
A balanced binary tree is a binary tree that follows the 3 conditions:

• The height of the left and right tree for any node does not differ by more than 1.
• The left subtree of that node is also balanced.
• The right subtree of that node is also balanced.

A single node is always balanced. It is also referred to as a height-balanced binary tree.

Example:

Balanced and Unbalanced Binary Tree

It is a type of binary tree in which the difference between the height of the left and the right subtree for each node is either 0 or 1. In the figure above, the root node having a value 0 is unbalanced with a depth of 2 units.

Application of Balanced Binary Tree:

• AVL Trees
• Red Black Tree
• Balanced Binary Search Tree

Advantages of Balanced Binary Tree:

• Non Destructive updates are supported by a Balanced Binary Tree with the same asymptotic effectiveness.
• Range queries and iteration in the right sequence are made feasible by the balanced binary tree.

Previous

Introduction to Height Balanced Binary Tree

Next

How to determine if a binary tree is height-balanced?

---

Preorder Traversal of Binary Tree =================================

**Preorder traversal** is defined as a type of **tree traversal** that follows the Root-Left-Right policy where:

• The root node of the subtree is visited first.
• Then the left subtree  is traversed.
• At last, the right subtree is traversed.

Preorder traversal

Algorithm for Preorder Traversal of Binary Tree

The algorithm for preorder traversal is shown as follows:

Preorder(root):

1. Follow step 2 to 4 until root != NULL
2. Write root -> data
3. Preorder (root -> left)
4. Preorder (root -> right)
5. End loop

How does Preorder Traversal of Binary Tree work?

Consider the following tree:

Example of Binary Tree

If we perform a preorder traversal in this binary tree, then the traversal will be as follows:

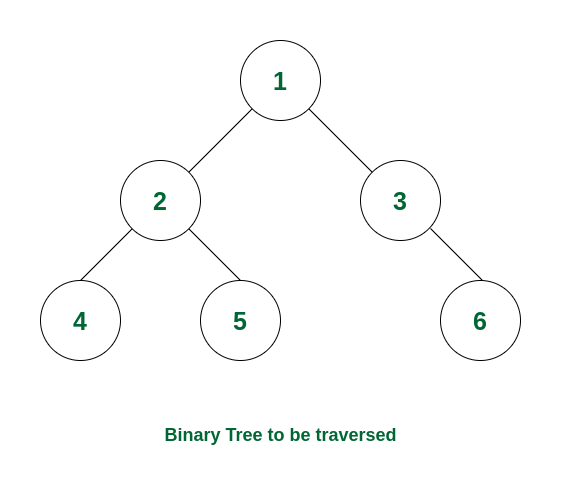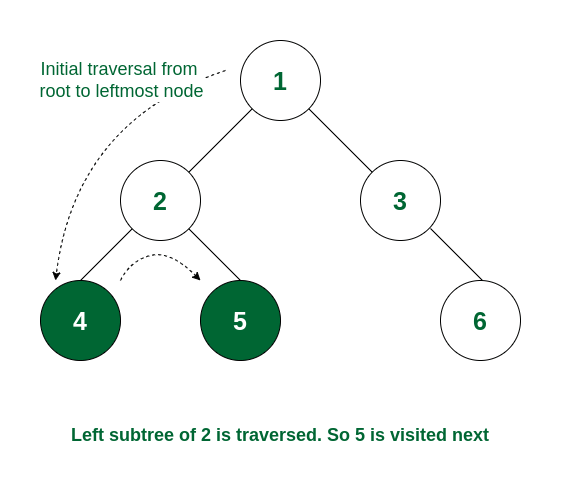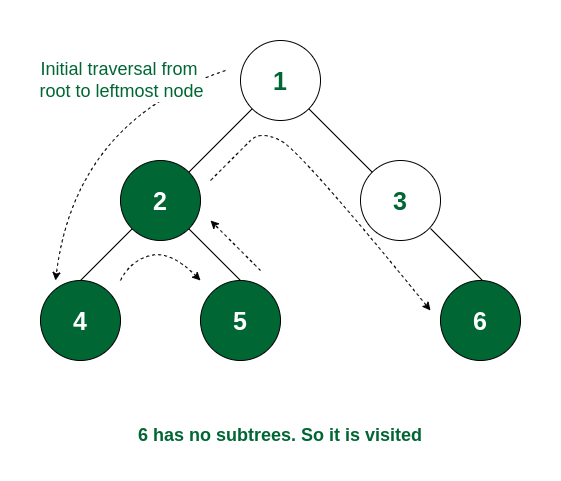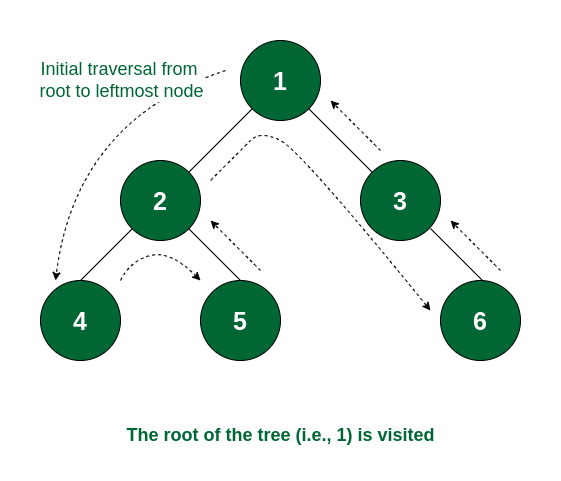
**Step 1:** At first the root will be visited, i.e. node 1.

Node 1 is visited

**Step 2:** After this, traverse in the left subtree. Now the root of the left subtree is visited i.e., node 2 is visited.

Node 2 is visited

**Step 3:** Again the left subtree of node 2 is traversed and the root of that subtree i.e., node 4 is visited.

Node 4 is visited

**Step 4:** There is no subtree of 4 and the left subtree of node 2 is visited. So now the right subtree of node 2 will be traversed and the root of that subtree i.e., node 5 will be visited.

Node 5 is visited

**Step 5:** The left subtree of node 1 is visited. So now the right subtree of node 1 will be traversed and the root node i.e., node 3 is visited.

Node 3 is visited

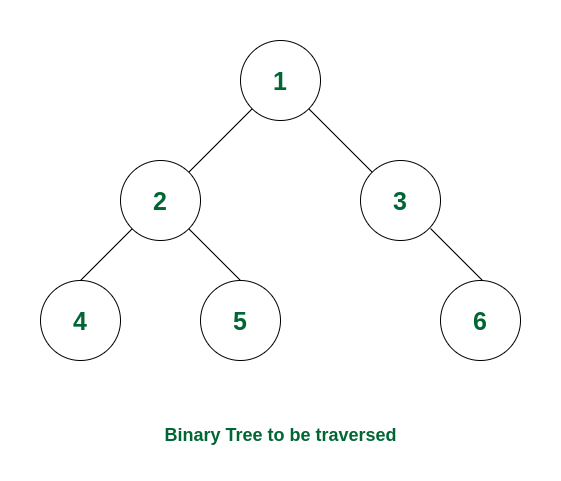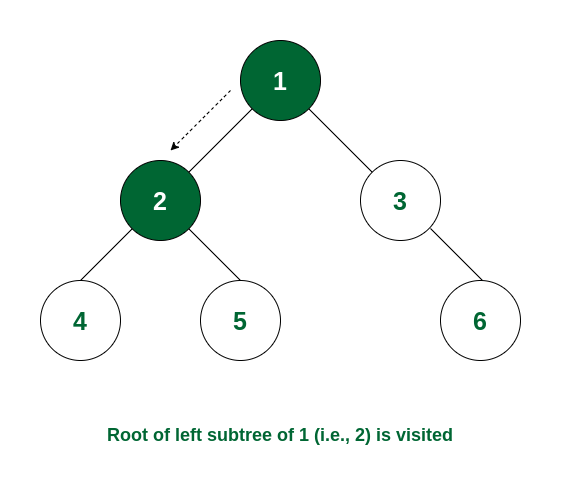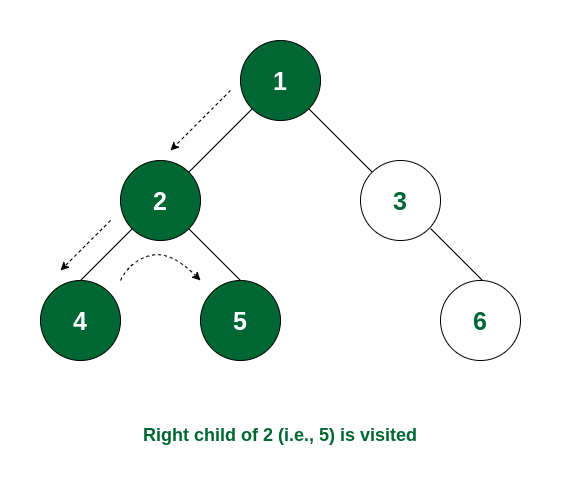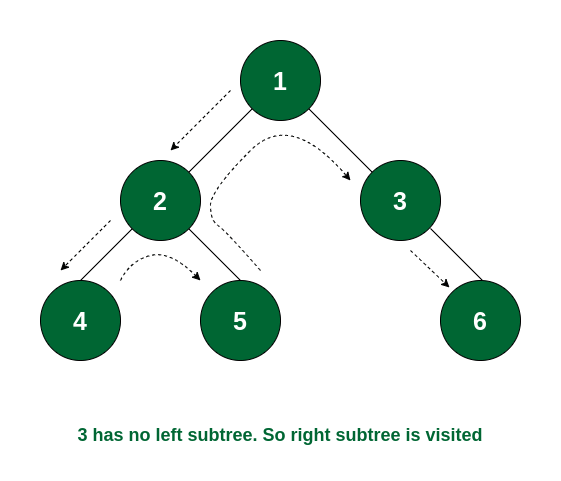
**Step 6:** Node 3 has no left subtree. So the right subtree will be traversed and the root of the subtree i.e., node 6 will be visited. After that there is no node that is not yet traversed. So the traversal ends.

The complete tree is visited

So the order of traversal of nodes is **1 -> 2 -> 4 -> 5 -> 3 -> 6**.

Program to Implement Preorder Traversal of Binary Tree

Below is the code implementation of the preorder traversal:

// C++ program for preorder traversals

#include <bits/stdc++.h>
using namespace std;

// Structure of a Binary Tree Node
struct Node {
    int data;
    struct Node *left, *right;
    Node(int v)
    {
        data = v;
        left = right = NULL;
    }
};

// Function to print preorder traversal
void printPreorder(struct Node* node)
{
    if (node == NULL)
        return;

    // Deal with the node
    cout << node->data << " ";

    // Recur on left subtree
    printPreorder(node->left);

    // Recur on right subtree
    printPreorder(node->right);
}

// Driver code
int main()
{
    struct Node* root = new Node(1);
    root->left = new Node(2);
    root->right = new Node(3);
    root->left->left = new Node(4);
    root->left->right = new Node(5);
    root->right->right = new Node(6);

    // Function call
    cout << "Preorder traversal of binary tree is: \n";
    printPreorder(root);

    return 0;
}

// Java program for preorder traversals

class Node {
    int data;
    Node left, right;

    public Node(int item) {
        data = item;
        left = right = null;
    }
}

class BinaryTree {
    Node root;

    BinaryTree() {
        root = null;
    }

    // Function to print preorder traversal
    void printPreorder(Node node) {
        if (node == null)
            return;

        // Deal with the node
        System.out.print(node.data + " ");

        // Recur on left subtree
        printPreorder(node.left);

        // Recur on right subtree
        printPreorder(node.right);
    }

    // Driver code
    public static void main(String[] args) {
        BinaryTree tree = new BinaryTree();

        // Constructing the binary tree
        tree.root = new Node(1);
        tree.root.left = new Node(2);
        tree.root.right = new Node(3);
        tree.root.left.left = new Node(4);
        tree.root.left.right = new Node(5);
        tree.root.right.right = new Node(6);

        // Function call
        System.out.println("Preorder traversal of binary tree is: ");
        tree.printPreorder(tree.root);
    }
}

Output

Preorder traversal of binary tree is: 
1 2 4 5 3 6 

**Explanation:**

How preorder traversal works

Complexity Analysis:

**Time Complexity:** O(N) where N is the total number of nodes. Because it traverses all the nodes at least once.
**Auxiliary Space:** 

• **O(1)** if no recursion stack space is considered.
• Otherwise, **O(h)** where h is the height of the tree
• In the worst case, **h** can be the same as **N** (when the tree is a skewed tree)
• In the best case, **h** can be the same as **logN** (when the tree is a complete tree)

Use cases of Preorder Traversal:

Some use cases of preorder traversal are:

• This is often used for creating a copy of a tree.
• It is also useful to get the prefix expression from an expression tree.

**Related Articles:**

• Types of Tree Traversal
• Iterative preorder traversal
• Check if given array can represent preorder traversal of BST
• Preorder from inorder and postorder traversals
• Find nth node in preorder traversal of a binary tree
• Preorder traversal of an N-ary tree

Next

Postorder Traversal of Binary Tree

---

Inorder Traversal of Binary Tree ================================

Inorder traversal is defined as a type of tree traversal technique which follows the Left-Root-Right pattern, such that:

• The left subtree is traversed first
• Then the root node for that subtree is traversed
• Finally, the right subtree is traversed

Inorder traversal

Algorithm for Inorder Traversal of Binary Tree

The algorithm for inorder traversal is shown as follows:

Inorder(root):

1. Follow step 2 to 4 until root != NULL
2. Inorder (root -> left)
3. Write root -> data
4. Inorder (root -> right)
5. End loop

How does Inorder Traversal of Binary Tree work?

Consider the following tree:

Example of Binary Tree

If we perform an inorder traversal in this binary tree, then the traversal will be as follows:

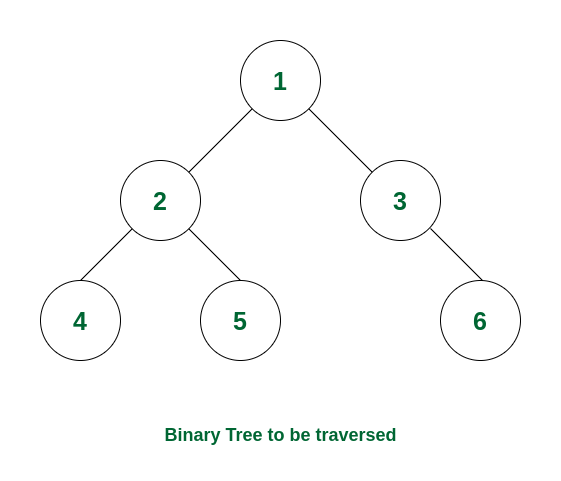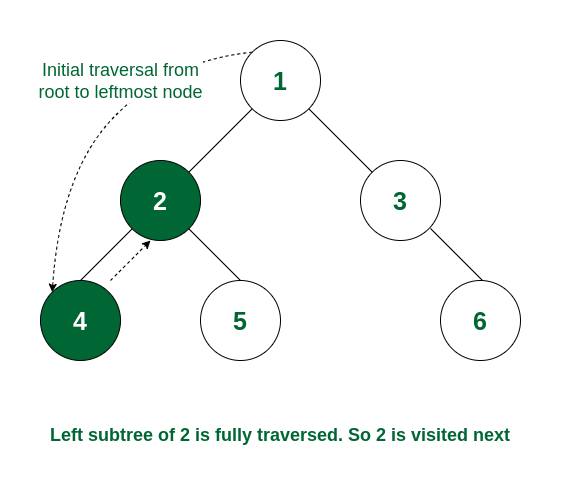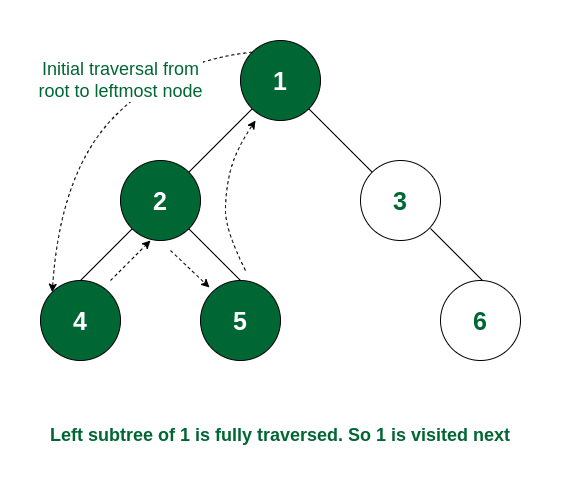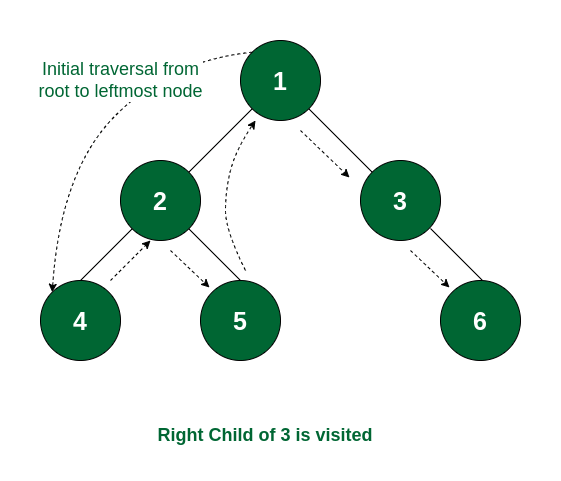
Step 1: The traversal will go from 1 to its left subtree i.e., 2, then from 2 to its left subtree root, i.e., 4. Now 4 has no left subtree, so it will be visited. It also does not have any right subtree. So no more traversal from 4

Node 4 is visited

Step 2: As the left subtree of 2 is visited completely, now it read data of node 2 before moving to its right subtree.

Node 2 is visited

Step 3: Now the right subtree of 2 will be traversed i.e., move to node 5. For node 5 there is no left subtree, so it gets visited and after that, the traversal comes back because there is no right subtree of node 5.

Node 5 is visited

Step 4: As the left subtree of node 1 is, the root itself, i.e., node 1 will be visited.

Node 1 is visited

Step 5: Left subtree of node 1 and the node itself is visited. So now the right subtree of 1 will be traversed i.e., move to node 3. As node 3 has no left subtree so it gets visited.

Node 3 is visited

Step 6: The left subtree of node 3 and the node itself is visited. So traverse to the right subtree and visit node 6. Now the traversal ends as all the nodes are traversed.

The complete tree is traversed

So the order of traversal of nodes is 4 -> 2 -> 5 -> 1 -> 3 -> 6.

Program to implement Inorder Traversal of Binary Tree:

Below is the code implementation of the inorder traversal:

C++

| // C++ program for inorder traversals   #include <bits/stdc++.h> using namespace std;   // Structure of a Binary Tree Node struct Node { int data; struct Node *left, *right; Node(int v) { data = v; left = right = NULL; } };   // Function to print inorder traversal void printInorder(struct Node* node) { if (node == NULL) return;   // First recur on left subtree printInorder(node->left);   // Now deal with the node cout << node->data << " ";   // Then recur on right subtree printInorder(node->right); }   // Driver code int main() { struct Node* root = new Node(1); root->left = new Node(2); root->right = new Node(3); root->left->left = new Node(4); root->left->right = new Node(5); root->right->right = new Node(6);   // Function call cout << "Inorder traversal of binary tree is: \n"; printInorder(root);   return 0; } | | — |

Java

| // Java program for inorder traversals import java.util.*;   // Structure of a Binary Tree Node class Node { int data; Node left, right;   Node(int v) { data = v; left = right = null; } }   // Main class class GFG {   // Function to print inorder traversal public static void printInorder(Node node) { if (node == null) return;   // First recur on left subtree printInorder(node.left);   // Now deal with the node System.out.print(node.data + " ");   // Then recur on right subtree printInorder(node.right); }   // Driver code public static void main(String[] args) { Node root = new Node(1); root.left = new Node(2); root.right = new Node(3); root.left.left = new Node(4); root.left.right = new Node(5); root.right.right = new Node(6);   // Function call System.out.println( "Inorder traversal of binary tree is: "); printInorder(root); } } // This code is contributed by prasad264 | | — |

Python3

| # Structure of a Binary Tree Node class Node: def __init__(self, v): self.data = v self.left = None self.right = None   # Function to print inorder traversal def printInorder(node): if node is None: return   # First recur on left subtree printInorder(node.left)   # Now deal with the node print(node.data, end=' ')   # Then recur on right subtree printInorder(node.right)   # Driver code if __name__ == '__main__': root = Node(1) root.left = Node(2) root.right = Node(3) root.left.left = Node(4) root.left.right = Node(5) root.right.right = Node(6)   # Function call print("Inorder traversal of binary tree is:") printInorder(root) | | — |

C#

| // C# program for inorder traversals   using System;   // Structure of a Binary Tree Node public class Node { public int data; public Node left, right;   public Node(int v) { data = v; left = right = null; } }   // Class to store and print inorder traversal public class BinaryTree { // Function to print inorder traversal public static void printInorder(Node node) { if (node == null) return;   // First recur on left subtree printInorder(node.left);   // Now deal with the node Console.Write(node.data + " ");   // Then recur on right subtree printInorder(node.right); }   // Driver code public static void Main() { Node root = new Node(1); root.left = new Node(2); root.right = new Node(3); root.left.left = new Node(4); root.left.right = new Node(5); root.right.right = new Node(6);   // Function call Console.WriteLine( "Inorder traversal of binary tree is: "); printInorder(root); } } | | — |

Javascript

| // JavaScript program for inorder traversals   // Structure of a Binary Tree Node class Node { constructor(v) { this.data = v; this.left = null; this.right = null; } }   // Function to print inorder traversal function printInorder(node) { if (node === null) { return; }   // First recur on left subtree printInorder(node.left);   // Now deal with the node console.log(node.data);   // Then recur on right subtree printInorder(node.right); }   // Driver code const root = new Node(1); root.left = new Node(2); root.right = new Node(3); root.left.left = new Node(4); root.left.right = new Node(5); root.right.right = new Node(6);   // Function call console.log("Inorder traversal of binary tree is: "); printInorder(root); | | — |

Output

Inorder traversal of binary tree is: 
4 2 5 1 3 6 

Explanation:

How inorder traversal works

Complexity Analysis:

Time Complexity: O(N) where N is the total number of nodes. Because it traverses all the nodes at least once.
Auxiliary Space: O(1) if no recursion stack space is considered. Otherwise, O(h) where h is the height of the tree

• In the worst case, h can be the same as N (when the tree is a skewed tree)
• In the best case, h can be the same as logN (when the tree is a complete tree)

Use cases of Inorder Traversal:

In the case of BST (Binary Search Tree), if any time there is a need to get the nodes in non-decreasing order, the best way is to implement an inorder traversal.

Related Articles:

• Types of Tree Traversals
• Iterative inorder traversal
• Construct binary tree from preorder and inorder traversal
• Morris traversal for inorder traversal of tree
• Inorder traversal without recursion

Next

Inorder traversal of an N-ary Tree

---

Postorder Traversal of Binary Tree ==================================

Postorder traversal is defined as a type of tree traversal which follows the Left-Right-Root policy such that for each node:

• The left subtree is traversed first
• Then the right subtree is traversed
• Finally, the root node of the subtree is traversed

Postorder traversal

Algorithm for Postorder Traversal of Binary Tree:

The algorithm for postorder traversal is shown as follows:

Postorder(root):

1. Follow step 2 to 4 until root != NULL
2. Postorder (root -> left)
3. Postorder (root -> right)
4. Write root -> data
5. End loop

How does Postorder Traversal of Binary Tree Work?

Consider the following tree:

Example of Binary Tree

If we perform a postorder traversal in this binary tree, then the traversal will be as follows:

Step 1: The traversal will go from 1 to its left subtree i.e., 2, then from 2 to its left subtree root, i.e., 4. Now 4 has no subtree, so it will be visited.

Node 4 is visited

Step 2: As the left subtree of 2 is visited completely, now it will traverse the right subtree of 2 i.e., it will move to 5. As there is no subtree of 5, it will be visited.

Node 5 is visited

Step 3: Now both the left and right subtrees of node 2 are visited. So now visit node 2 itself.

Node 2 is visited

Step 4: As the left subtree of node 1 is traversed, it will now move to the right subtree root, i.e., 3. Node 3 does not have any left subtree, so it will traverse the right subtree i.e., 6. Node 6 has no subtree and so it is visited.

Node 6 is visited

Step 5: All the subtrees of node 3 are traversed. So now node 3 is visited.

Node 3 is visited

Step 6: As all the subtrees of node 1 are traversed, now it is time for node 1 to be visited and the traversal ends after that as the whole tree is traversed.

The complete tree is visited

So the order of traversal of nodes is 4 -> 5 -> 2 -> 6 -> 3 -> 1.

Program to implement Postorder Traversal of Binary Tree

Below is the code implementation of the postorder traversal:

C++

| // C++ program for postorder traversals   #include <bits/stdc++.h> using namespace std;   // Structure of a Binary Tree Node struct Node { int data; struct Node *left, *right; Node(int v) { data = v; left = right = NULL; } };   // Function to print postorder traversal void printPostorder(struct Node* node) { if (node == NULL) return;   // First recur on left subtree printPostorder(node->left);   // Then recur on right subtree printPostorder(node->right);   // Now deal with the node cout << node->data << " "; }   // Driver code int main() { struct Node* root = new Node(1); root->left = new Node(2); root->right = new Node(3); root->left->left = new Node(4); root->left->right = new Node(5); root->right->right = new Node(6);   // Function call cout << "Postorder traversal of binary tree is: \n"; printPostorder(root);   return 0; } | | — |

Java

| // Java program for postorder traversals import java.util.*;   // Structure of a Binary Tree Node class Node { int data; Node left, right; Node(int v) { data = v; left = right = null; } }   class GFG {   // Function to print postorder traversal static void printPostorder(Node node) { if (node == null) return;   // First recur on left subtree printPostorder(node.left);   // Then recur on right subtree printPostorder(node.right);   // Now deal with the node System.out.print(node.data + " "); }   // Driver code public static void main(String[] args) { Node root = new Node(1); root.left = new Node(2); root.right = new Node(3); root.left.left = new Node(4); root.left.right = new Node(5); root.right.right = new Node(6);   // Function call System.out.println("Postorder traversal of binary tree is: "); printPostorder(root); } } // This code is contributed by prasad264 | | — |

Python3

| # Python program for postorder traversals   # Structure of a Binary Tree Node     class Node: def __init__(self, v): self.data = v self.left = None self.right = None   # Function to print postorder traversal     def printPostorder(node): if node == None: return   # First recur on left subtree printPostorder(node.left)   # Then recur on right subtree printPostorder(node.right)   # Now deal with the node print(node.data, end=' ')     # Driver code if __name__ == '__main__': root = Node(1) root.left = Node(2) root.right = Node(3) root.left.left = Node(4) root.left.right = Node(5) root.right.right = Node(6)   # Function call print("Postorder traversal of binary tree is:") printPostorder(root) | | — |

C#

| // C# program for postorder traversals   using System;   // Structure of a Binary Tree Node public class Node { public int data; public Node left, right; public Node(int v) { data = v; left = right = null; } }   public class GFG {   // Function to print postorder traversal static void printPostorder(Node node) { if (node == null) return;   // First recur on left subtree printPostorder(node.left);   // Then recur on right subtree printPostorder(node.right);   // Now deal with the node Console.Write(node.data + " "); }   static public void Main() {   // Code Node root = new Node(1); root.left = new Node(2); root.right = new Node(3); root.left.left = new Node(4); root.left.right = new Node(5); root.right.right = new Node(6);   // Function call Console.WriteLine( "Postorder traversal of binary tree is: "); printPostorder(root); } }   // This code is contributed by karthik. | | — |

Javascript

| // Structure of a Binary Tree Node class Node { constructor(v) { this.data = v; this.left = null; this.right = null; } }   // Function to print postorder traversal function printPostorder(node) { if (node == null) { return; }   // First recur on left subtree printPostorder(node.left);   // Then recur on right subtree printPostorder(node.right);   // Now deal with the node console.log(node.data + " "); }   // Driver code function main() { let root = new Node(1); root.left = new Node(2); root.right = new Node(3); root.left.left = new Node(4); root.left.right = new Node(5); root.right.right = new Node(6);   // Function call console.log("Postorder traversal of binary tree is: \n"); printPostorder(root); }   main(); | | — |

Output

Postorder traversal of binary tree is: 
4 5 2 6 3 1 

Explanation:

How postorder traversal works

Complexity Analysis:

Time Complexity: O(N) where N is the total number of nodes. Because it traverses all the nodes at least once.
Auxiliary Space: O(1) if no recursion stack space is considered. Otherwise, O(h) where h is the height of the tree

• In the worst case, h can be the same as N (when the tree is a skewed tree)
• In the best case, h can be the same as logN (when the tree is a complete tree)

Use cases of Postorder Traversal:

Some use cases of postorder traversal are:

• This is used for tree deletion.
• It is also useful to get the postfix expression from an expression tree.

Related articles:

• Types of Tree traversals
• Iterative Postorder traversal (using two stacks)
• Iterative Postorder traversal (using one stack)
• Postorder of Binary Tree without recursion and without stack
• Find Postorder traversal of BST from preorder traversal
• Morris traversal for Postorder
• Print postorder traversal from preoreder and inorder traversal

Next

Preorder Traversal of Binary Tree

---

Level Order Traversal (Breadth First Search or BFS) of Binary Tree ==================================================================

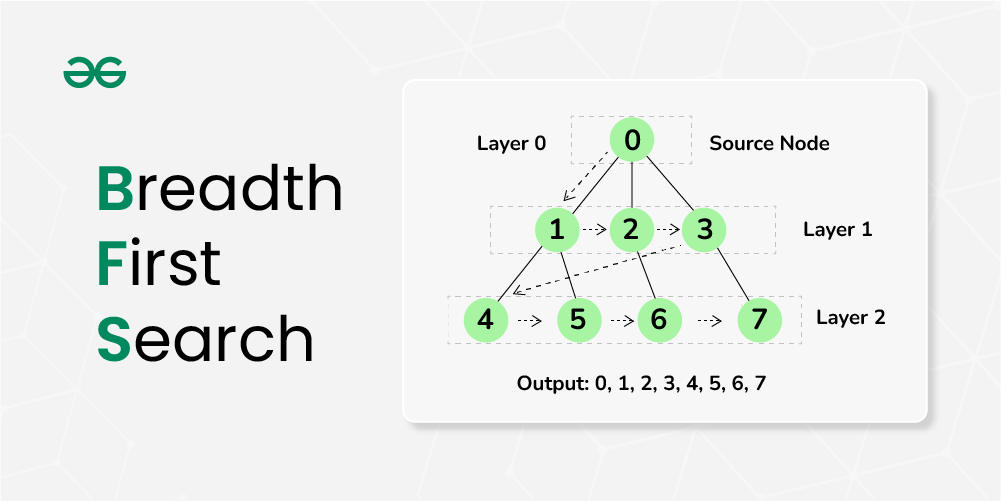
**Level Order Traversal** technique is defined as a method to traverse a Tree such that all nodes present in the same level are traversed completely before traversing the next level.

**Example:**

**Input:**

**Output:**
1
2 3
4 5

Recommended PracticeLevel order traversalTry It!How does Level Order Traversal work?

The main idea of level order traversal is to traverse all the nodes of a lower level before moving to any of the nodes of a higher level. This can be done in any of the following ways: 

• the naive one (finding the height of the tree and traversing each level and printing the nodes of that level)
• efficiently using a queue.

Level Order Traversal (Naive approach):

Find **height** of tree. Then for each level, run a recursive function by maintaining current height. Whenever the level of a node matches, print that node.

Below is the implementation of the above approach:

// Recursive CPP program for level
// order traversal of Binary Tree
#include <bits/stdc++.h>
using namespace std;

// A binary tree node has data,
// pointer to left child
// and a pointer to right child
class node {
public:
    int data;
    node *left, *right;
};

// Function prototypes
void printCurrentLevel(node* root, int level);
int height(node* node);
node* newNode(int data);

// Function to print level order traversal a tree
void printLevelOrder(node* root)
{
    int h = height(root);
    int i;
    for (i = 1; i <= h; i++)
        printCurrentLevel(root, i);
}

// Print nodes at a current level
void printCurrentLevel(node* root, int level)
{
    if (root == NULL)
        return;
    if (level == 1)
        cout << root->data << " ";
    else if (level > 1) {
        printCurrentLevel(root->left, level - 1);
        printCurrentLevel(root->right, level - 1);
    }
}

// Compute the "height" of a tree -- the number of
// nodes along the longest path from the root node
// down to the farthest leaf node.
int height(node* node)
{
    if (node == NULL)
        return 0;
    else {
        
        // Compute the height of each subtree
        int lheight = height(node->left);
        int rheight = height(node->right);

        // Use the larger one
        if (lheight > rheight) {
            return (lheight + 1);
        }
        else {
            return (rheight + 1);
        }
    }
}

// Helper function that allocates
// a new node with the given data and
// NULL left and right pointers.
node* newNode(int data)
{
    node* Node = new node();
    Node->data = data;
    Node->left = NULL;
    Node->right = NULL;

    return (Node);
}

// Driver code
int main()
{
    node* root = newNode(1);
    root->left = newNode(2);
    root->right = newNode(3);
    root->left->left = newNode(4);
    root->left->right = newNode(5);

    cout << "Level Order traversal of binary tree is \n";
    printLevelOrder(root);

    return 0;
}

// This code is contributed by rathbhupendra

// Recursive Java program for level
// order traversal of Binary Tree

// Class containing left and right child of current
// node and key value
class Node {
    int data;
    Node left, right;
    public Node(int item)
    {
        data = item;
        left = right = null;
    }
}

class BinaryTree {
    
    // Root of the Binary Tree
    Node root;

    public BinaryTree() { root = null; }

    // Function to print level order traversal of tree
    void printLevelOrder()
    {
        int h = height(root);
        int i;
        for (i = 1; i <= h; i++)
            printCurrentLevel(root, i);
    }

    // Compute the "height" of a tree -- the number of
    // nodes along the longest path from the root node
    // down to the farthest leaf node.
    int height(Node root)
    {
        if (root == null)
            return 0;
        else {
            
            // Compute  height of each subtree
            int lheight = height(root.left);
            int rheight = height(root.right);

            // use the larger one
            if (lheight > rheight)
                return (lheight + 1);
            else
                return (rheight + 1);
        }
    }

    // Print nodes at the current level
    void printCurrentLevel(Node root, int level)
    {
        if (root == null)
            return;
        if (level == 1)
            System.out.print(root.data + " ");
        else if (level > 1) {
            printCurrentLevel(root.left, level - 1);
            printCurrentLevel(root.right, level - 1);
        }
    }

    // Driver program to test above functions
    public static void main(String args[])
    {
        BinaryTree tree = new BinaryTree();
        tree.root = new Node(1);
        tree.root.left = new Node(2);
        tree.root.right = new Node(3);
        tree.root.left.left = new Node(4);
        tree.root.left.right = new Node(5);

        System.out.println("Level order traversal of"
                           + "binary tree is ");
        tree.printLevelOrder();
    }
}

Output

Level Order traversal of binary tree is 
1 2 3 4 5 

**Time Complexity:** O(N), where N is the number of nodes in the skewed tree.
**Auxiliary Space:** O(1) If the recursion stack is considered the space used is O(N).

Level Order Traversal using Queue

We need to visit the nodes in a lower level before any node in a higher level, this idea is quite similar to that of a queue. Push the nodes of a lower level in the queue. When any node is visited, pop that node from the queue and push the child of that node in the queue.

This ensures that the node of a lower level are visited prior to any node of a higher level.

Below is the Implementation of the above approach:

// C++ program to print level order traversal
#include <bits/stdc++.h>
using namespace std;

// A Binary Tree Node
struct Node {
    int data;
    struct Node *left, *right;
};

// Iterative method to find height of Binary Tree
void printLevelOrder(Node* root)
{
    // Base Case
    if (root == NULL)
        return;

    // Create an empty queue for level order traversal
    queue<Node*> q;

    // Enqueue Root and initialize height
    q.push(root);

    while (q.empty() == false) {
        
        // Print front of queue and remove it from queue
        Node* node = q.front();
        cout << node->data << " ";
        q.pop();

        // Enqueue left child
        if (node->left != NULL)
            q.push(node->left);

        // Enqueue right child
        if (node->right != NULL)
            q.push(node->right);
    }
}

// Utility function to create a new tree node
Node* newNode(int data)
{
    Node* temp = new Node;
    temp->data = data;
    temp->left = temp->right = NULL;
    return temp;
}

// Driver program to test above functions
int main()
{
    // Let us create binary tree shown in above diagram
    Node* root = newNode(1);
    root->left = newNode(2);
    root->right = newNode(3);
    root->left->left = newNode(4);
    root->left->right = newNode(5);

    cout << "Level Order traversal of binary tree is \n";
    printLevelOrder(root);
    return 0;
}

// Iterative Queue based Java program
// to do level order traversal
// of Binary Tree

import java.util.LinkedList;
import java.util.Queue;

// Class to represent Tree node
class Node {
    int data;
    Node left, right;

    public Node(int item)
    {
        data = item;
        left = null;
        right = null;
    }
}

// Class to print Level Order Traversal
class BinaryTree {

    Node root;

    // Given a binary tree. Print
    // its nodes in level order
    // using array for implementing queue
    void printLevelOrder()
    {
        Queue<Node> queue = new LinkedList<Node>();
        queue.add(root);
        while (!queue.isEmpty()) {

            // poll() removes the present head.  
            Node tempNode = queue.poll();
            System.out.print(tempNode.data + " ");

            // Enqueue left child
            if (tempNode.left != null) {
                queue.add(tempNode.left);
            }

            // Enqueue right child
            if (tempNode.right != null) {
                queue.add(tempNode.right);
            }
        }
    }

    public static void main(String args[])
    {
        // Creating a binary tree and entering
        // the nodes
        BinaryTree tree_level = new BinaryTree();
        tree_level.root = new Node(1);
        tree_level.root.left = new Node(2);
        tree_level.root.right = new Node(3);
        tree_level.root.left.left = new Node(4);
        tree_level.root.left.right = new Node(5);

        System.out.println("Level order traversal of binary tree is - ");
        tree_level.printLevelOrder();
    }
}

Output

Level Order traversal of binary tree is 
1 2 3 4 5 

**Time Complexity:** O(N) where N is the number of nodes in the binary tree.
**Auxiliary Space:** O(N) where N is the number of nodes in the binary tree.

Previous

Perfect Binary Tree

Next

Level order traversal in spiral form

---

AVL Tree Data Structure =======================

An **AVL tree** defined as a self-balancing **Binary Search Tree** (BST) where the difference between heights of left and right subtrees for any node cannot be more than one.

The difference between the heights of the left subtree and the right subtree for any node is known as the **balance factor** of the node.

The AVL tree is named after its inventors, Georgy Adelson-Velsky and Evgenii Landis, who published it in their 1962 paper “An algorithm for the organization of information”.

Example of AVL Trees:

AVL tree

The above tree is AVL because the differences between the heights of left and right subtrees for every node are less than or equal to 1.

Operations on an AVL Tree:

• Insertion
• Deletion
• Searching [It is similar to performing a search in BST]

Rotating the subtrees in an AVL Tree:

An AVL tree may rotate in one of the following four ways to keep itself balanced:

**Left Rotation**:

When a node is added into the right subtree of the right subtree, if the tree gets out of balance, we do a single left rotation.

Left-Rotation in AVL tree

**Right Rotation**:

If a node is added to the left subtree of the left subtree, the AVL tree may get out of balance, we do a single right rotation.

Right-Rotation in AVL Tree

**Left-Right Rotation**:

A left-right rotation is a combination in which first left rotation takes place after that right rotation executes.

Left-Right Rotation in AVL tree

**Right-Left Rotation**:

A right-left rotation is a combination in which first right rotation takes place after that left rotation executes.

Right-Left Rotation in AVL tree

Applications of AVL Tree:

1. It is used to index huge records in a database and also to efficiently search in that.
2. For all types of in-memory collections, including sets and dictionaries, AVL Trees are used.
3. Database applications, where insertions and deletions are less common but frequent data lookups are necessary
4. Software that needs optimized search.
5. It is applied in corporate areas and storyline games.

Advantages of AVL Tree:

1. AVL trees can self-balance themselves.
2. It is surely not skewed.
3. It provides faster lookups than Red-Black Trees
4. Better searching time complexity compared to other trees like binary tree.
5. Height cannot exceed log(N), where, N is the total number of nodes in the tree.

Disadvantages of AVL Tree:

1. It is difficult to implement.
2. It has high constant factors for some of the operations.
3. Less used compared to Red-Black trees.
4. Due to its rather strict balance, AVL trees provide complicated insertion and removal operations as more rotations are performed.
5. Take more processing for balancing.

**Related Articles:**

• Introduction to Binary Search Trees – Data Structure and Algorithm Tutorials
• Insertion in an AVL Tree
• Deletion in an AVL Tree

Next

[What is AVL Tree

AVL Tree meaning](https://www.geeksforgeeks.org/what-is-avl-tree-avl-tree-meaning/?ref=next_article)

---

Insertion in an AVL Tree ========================

AVL Tree:

AVL tree is a self-balancing Binary Search Tree (BST) where the difference between heights of left and right subtrees cannot be more than one for all nodes. 

Example of AVL Tree:

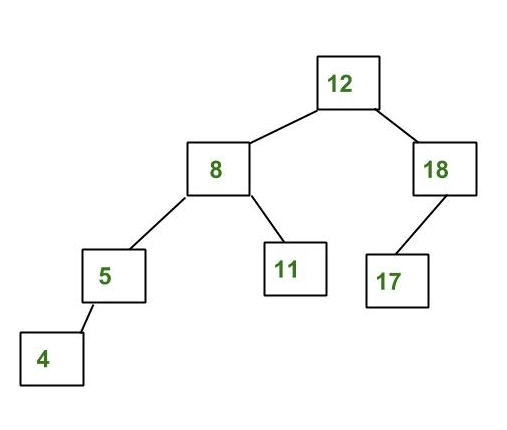
The above tree is AVL because the differences between the heights of left and right subtrees for every node are less than or equal to 1.

Example of a Tree that is NOT an AVL Tree:

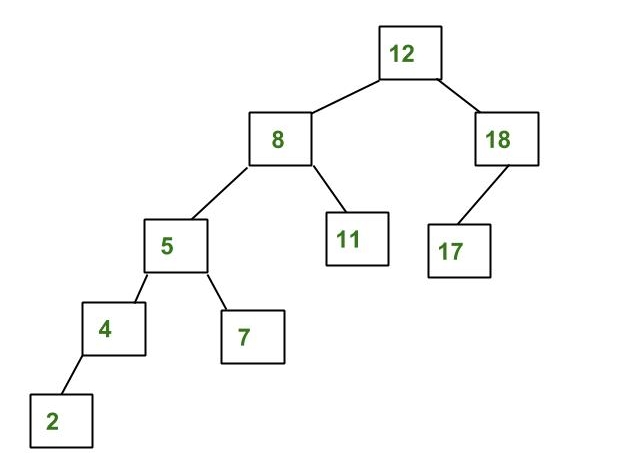
The above tree is not AVL because the differences between the heights of the left and right subtrees for 8 and 12 are greater than 1.

Why AVL Trees?

Most of the BST operations (e.g., search, max, min, insert, delete.. etc) take O(h) time where h is the height of the BST. The cost of these operations may become O(n) for a skewed Binary tree. If we make sure that the height of the tree remains O(log(n)) after every insertion and deletion, then we can guarantee an upper bound of O(log(n)) for all these operations. The height of an AVL tree is always O(log(n)) where n is the number of nodes in the tree.

Insertion in AVL Tree:

To make sure that the given tree remains AVL after every insertion, we must augment the standard BST insert operation to perform some re-balancing. 
Following are two basic operations that can be performed to balance a BST without violating the BST property (keys(left) < key(root) < keys(right)). 

• Left Rotation
• Right Rotation

T1, T2 and T3 are subtrees of the tree, rooted with y (on the left side) or x (on the right side)     
      
     y                               x
    / \     Right Rotation          /  \
   x   T3   - - - - - - - >        T1   y 
  / \       < - - - - - - -            / \
 T1  T2     Left Rotation            T2  T3
 
Keys in both of the above trees follow the following order 
keys(T1) < key(x) < keys(T2) < key(y) < keys(T3)
So BST property is not violated anywhere.

Recommended Practice AVL Tree Insertion

Try It!

Steps to follow for insertion:

Let the newly inserted node be w 

• Perform standard BST insert for w.
• Starting from w, travel up and find the first unbalanced node. Let z be the first unbalanced node, y be the child of z that comes on the path from w to z and x be the grandchild of z that comes on the path from w to z.
• Re-balance the tree by performing appropriate rotations on the subtree rooted with z. There can be 4 possible cases that need to be handled as x, y and z can be arranged in 4 ways.
• Following are the possible 4 arrangements:
  • y is the left child of z and x is the left child of y (Left Left Case)
  • y is the left child of z and x is the right child of y (Left Right Case)
  • y is the right child of z and x is the right child of y (Right Right Case)
  • y is the right child of z and x is the left child of y (Right Left Case)

Following are the operations to be performed in above mentioned 4 cases. In all of the cases, we only need to re-balance the subtree rooted with z and the complete tree becomes balanced as the height of the subtree (After appropriate rotations) rooted with z becomes the same as it was before insertion.

1. Left Left Case 

T1, T2, T3 and T4 are subtrees.
         z                                      y 
        / \                                   /   \
       y   T4      Right Rotate (z)          x      z
      / \          - - - - - - - - ->      /  \    /  \ 
     x   T3                               T1  T2  T3  T4
    / \
  T1   T2

2. Left Right Case 

     z                               z                           x
    / \                            /   \                        /  \ 
   y   T4  Left Rotate (y)        x    T4  Right Rotate(z)    y      z
  / \      - - - - - - - - ->    /  \      - - - - - - - ->  / \    / \
T1   x                          y    T3                    T1  T2 T3  T4
    / \                        / \
  T2   T3                    T1   T2

3. Right Right Case 

  z                                y
 /  \                            /   \ 
T1   y     Left Rotate(z)       z      x
    /  \   - - - - - - - ->    / \    / \
   T2   x                     T1  T2 T3  T4
       / \
     T3  T4

4. Right Left Case 

   z                            z                            x
  / \                          / \                          /  \ 
T1   y   Right Rotate (y)    T1   x      Left Rotate(z)   z      y
    / \  - - - - - - - - ->     /  \   - - - - - - - ->  / \    / \
   x   T4                      T2   y                  T1  T2  T3  T4
  / \                              /  \
T2   T3                           T3   T4

Illustration of Insertion at AVL Tree

 

 

 

 

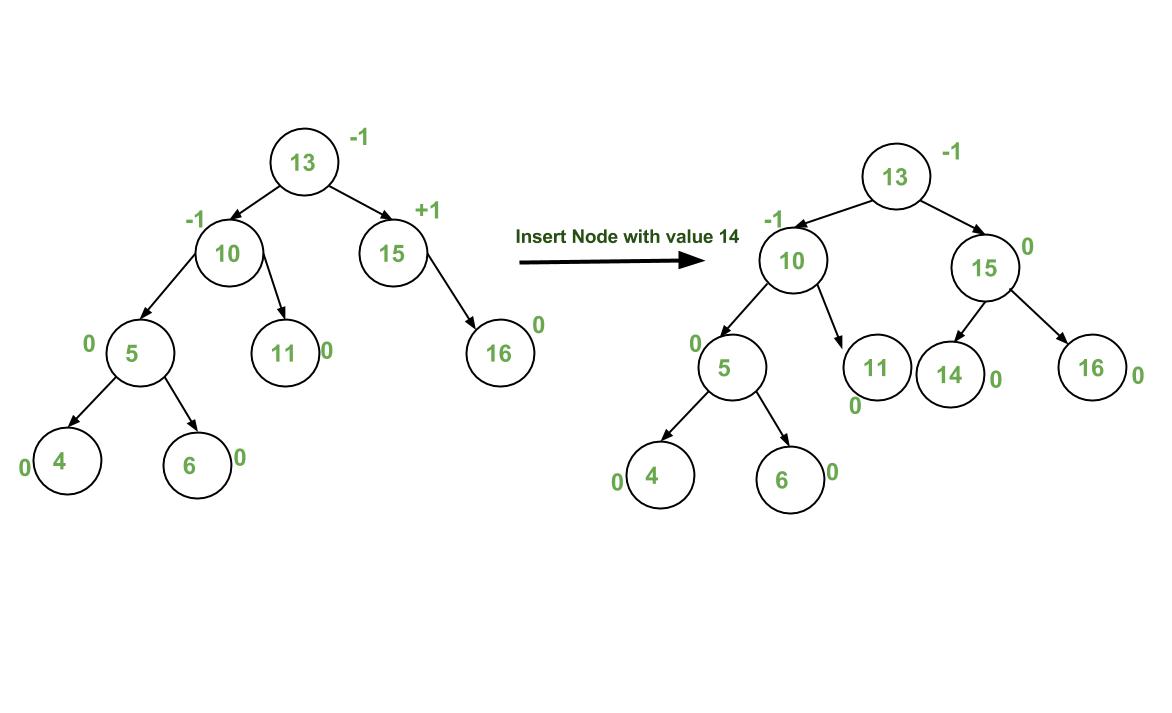
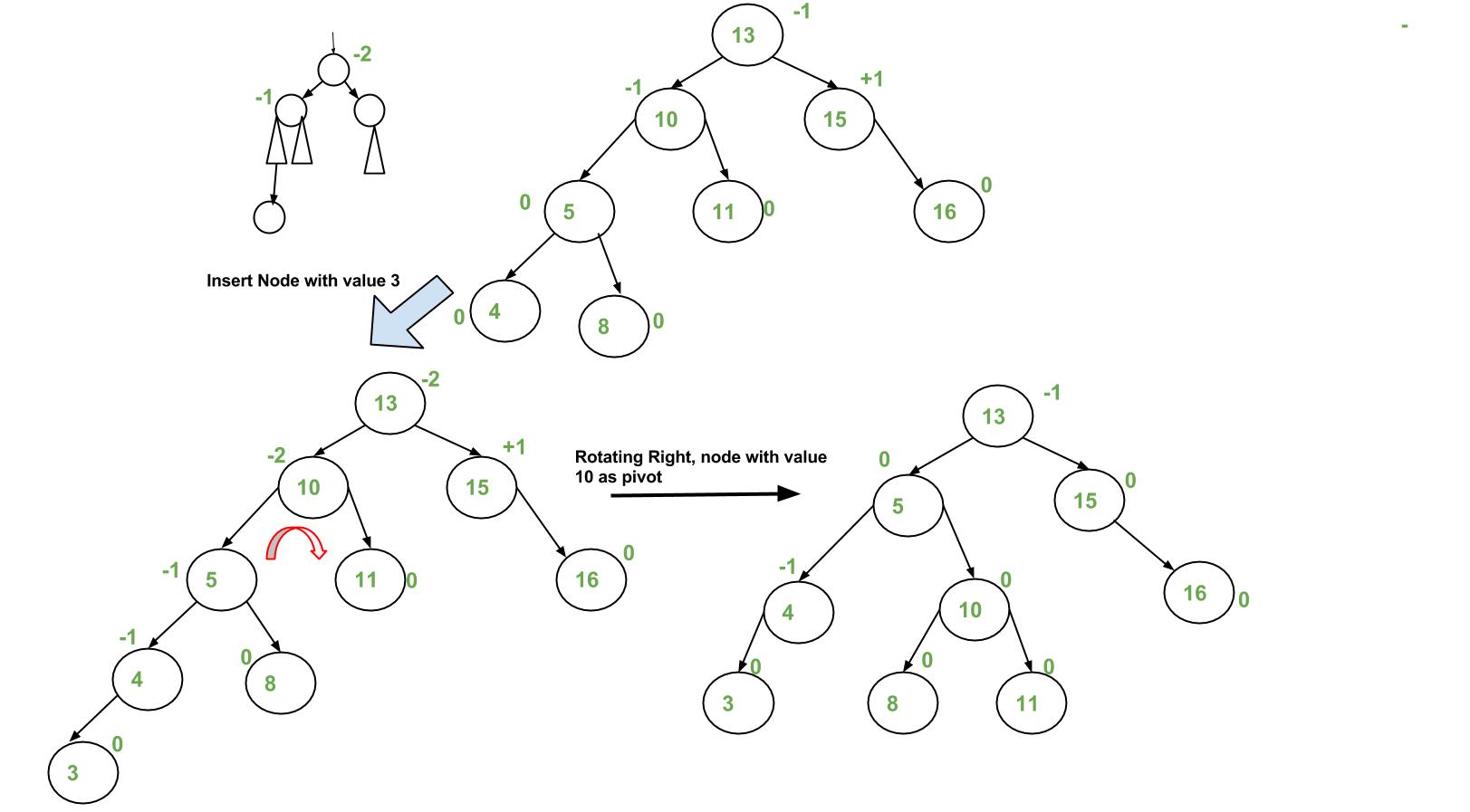
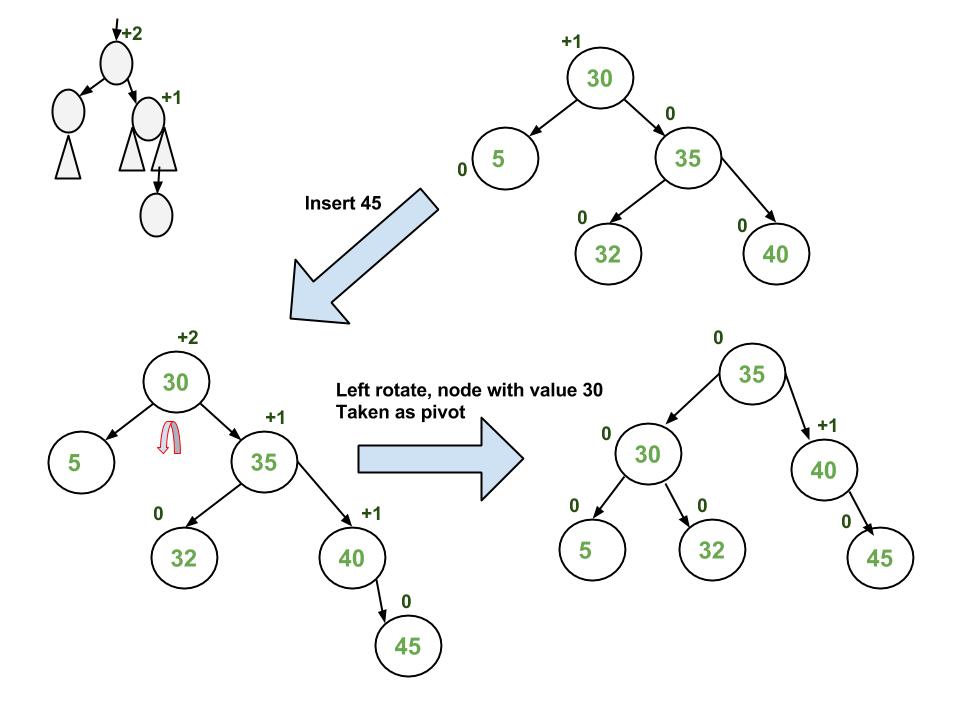
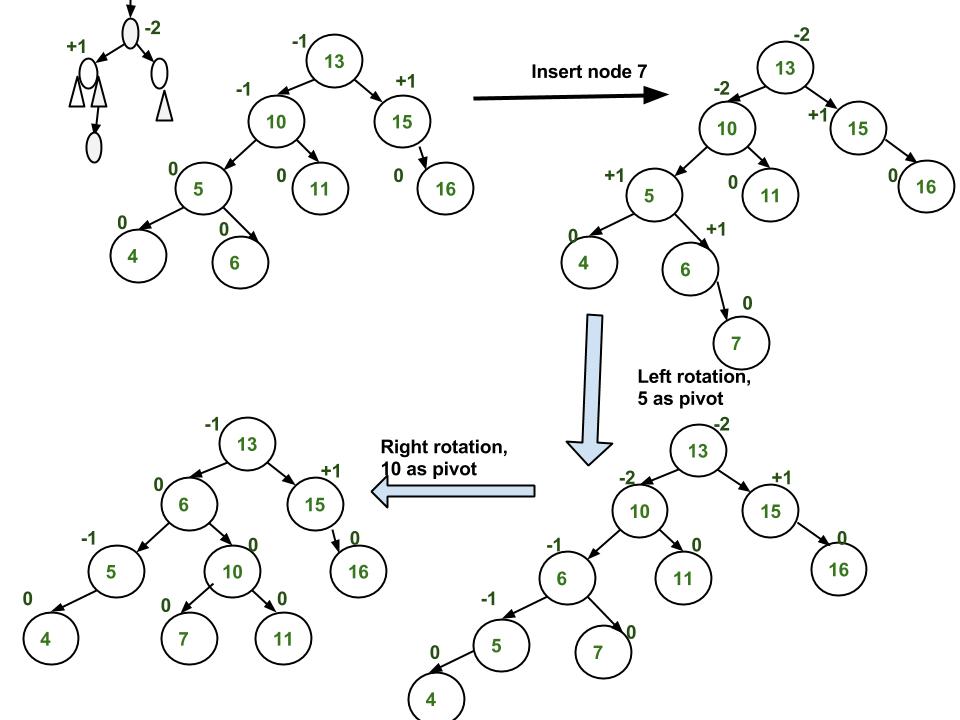
Approach:

The idea is to use recursive BST insert, after insertion, we get pointers to all ancestors one by one in a bottom-up manner. So we don’t need a parent pointer to travel up. The recursive code itself travels up and visits all the ancestors of the newly inserted node.

Follow the steps mentioned below to implement the idea:

• Perform the normalBST insertion.
• The current node must be one of the ancestors of the newly inserted node. Update the height of the current node.
• Get the balance factor (left subtree height – right subtree height) of the current node.
• If the balance factor is greater than 1, then the current node is unbalanced and we are either in the Left Left case or left Right case. To check whether it is left left case or not, compare the newly inserted key with the key in the left subtree root.
• If the balance factor is less than -1, then the current node is unbalanced and we are either in the Right Right case or Right-Left case. To check whether it is the Right Right case or not, compare the newly inserted key with the key in the right subtree root.

Below is the implementation of the above approach:

C++14

| // C++ program to insert a node in AVL tree #include<bits/stdc++.h> using namespace std;   // An AVL tree node class Node { public: int key; Node *left; Node *right; int height; };   // A utility function to get the // height of the tree int height(Node *N) { if (N == NULL) return 0; return N->height; }   // A utility function to get maximum // of two integers int max(int a, int b) { return (a > b)? a : b; }   /* Helper function that allocates a new node with the given key and NULL left and right pointers. */ Node* newNode(int key) { Node* node = new Node(); node->key = key; node->left = NULL; node->right = NULL; node->height = 1; // new node is initially // added at leaf return(node); }   // A utility function to right // rotate subtree rooted with y // See the diagram given above. Node *rightRotate(Node *y) { Node *x = y->left; Node *T2 = x->right;   // Perform rotation x->right = y; y->left = T2;   // Update heights y->height = max(height(y->left), height(y->right)) + 1; x->height = max(height(x->left), height(x->right)) + 1;   // Return new root return x; }   // A utility function to left // rotate subtree rooted with x // See the diagram given above. Node *leftRotate(Node *x) { Node *y = x->right; Node *T2 = y->left;   // Perform rotation y->left = x; x->right = T2;   // Update heights x->height = max(height(x->left), height(x->right)) + 1; y->height = max(height(y->left), height(y->right)) + 1;   // Return new root return y; }   // Get Balance factor of node N int getBalance(Node *N) { if (N == NULL) return 0; return height(N->left) - height(N->right); }   // Recursive function to insert a key // in the subtree rooted with node and // returns the new root of the subtree. Node* insert(Node* node, int key) { /* 1. Perform the normal BST insertion */ if (node == NULL) return(newNode(key));   if (key < node->key) node->left = insert(node->left, key); else if (key > node->key) node->right = insert(node->right, key); else // Equal keys are not allowed in BST return node;   /* 2. Update height of this ancestor node */ node->height = 1 + max(height(node->left), height(node->right));   /* 3. Get the balance factor of this ancestor node to check whether this node became unbalanced */ int balance = getBalance(node);   // If this node becomes unbalanced, then // there are 4 cases   // Left Left Case if (balance > 1 && key < node->left->key) return rightRotate(node);   // Right Right Case if (balance < -1 && key > node->right->key) return leftRotate(node);   // Left Right Case if (balance > 1 && key > node->left->key) { node->left = leftRotate(node->left); return rightRotate(node); }   // Right Left Case if (balance < -1 && key < node->right->key) { node->right = rightRotate(node->right); return leftRotate(node); }   /* return the (unchanged) node pointer */ return node; }   // A utility function to print preorder // traversal of the tree. // The function also prints height // of every node void preOrder(Node *root) { if(root != NULL) { cout << root->key << " "; preOrder(root->left); preOrder(root->right); } }   // Driver Code int main() { Node *root = NULL;   /* Constructing tree given in the above figure */ root = insert(root, 10); root = insert(root, 20); root = insert(root, 30); root = insert(root, 40); root = insert(root, 50); root = insert(root, 25);   /* The constructed AVL Tree would be 30 / \ 20 40 / \ \ 10 25 50 */ cout << "Preorder traversal of the " "constructed AVL tree is \n"; preOrder(root);   return 0; }   // This code is contributed by // rathbhupendra | | — |

C

| // C program to insert a node in AVL tree #include<stdio.h> #include<stdlib.h>   // An AVL tree node struct Node { int key; struct Node *left; struct Node *right; int height; };   // A utility function to get the height of the tree int height(struct Node *N) { if (N == NULL) return 0; return N->height; }   // A utility function to get maximum of two integers int max(int a, int b) { return (a > b)? a : b; }   /* Helper function that allocates a new node with the given key and NULL left and right pointers. */ struct Node* newNode(int key) { struct Node* node = (struct Node*) malloc(sizeof(struct Node)); node->key   = key; node->left   = NULL; node->right  = NULL; node->height = 1; // new node is initially added at leaf return(node); }   // A utility function to right rotate subtree rooted with y // See the diagram given above. struct Node *rightRotate(struct Node *y) { struct Node *x = y->left; struct Node *T2 = x->right;   // Perform rotation x->right = y; y->left = T2;   // Update heights y->height = max(height(y->left), height(y->right)) + 1; x->height = max(height(x->left), height(x->right)) + 1;   // Return new root return x; }   // A utility function to left rotate subtree rooted with x // See the diagram given above. struct Node *leftRotate(struct Node *x) { struct Node *y = x->right; struct Node *T2 = y->left;   // Perform rotation y->left = x; x->right = T2;   //  Update heights x->height = max(height(x->left), height(x->right)) + 1; y->height = max(height(y->left), height(y->right)) + 1;   // Return new root return y; }   // Get Balance factor of node N int getBalance(struct Node *N) { if (N == NULL) return 0; return height(N->left) - height(N->right); }   // Recursive function to insert a key in the subtree rooted // with node and returns the new root of the subtree. struct Node* insert(struct Node* node, int key) { /* 1.  Perform the normal BST insertion */ if (node == NULL) return(newNode(key));   if (key < node->key) node->left  = insert(node->left, key); else if (key > node->key) node->right = insert(node->right, key); else // Equal keys are not allowed in BST return node;   /* 2. Update height of this ancestor node */ node->height = 1 + max(height(node->left), height(node->right));   /* 3. Get the balance factor of this ancestor node to check whether this node became unbalanced */ int balance = getBalance(node);   // If this node becomes unbalanced, then // there are 4 cases   // Left Left Case if (balance > 1 && key < node->left->key) return rightRotate(node);   // Right Right Case if (balance < -1 && key > node->right->key) return leftRotate(node);   // Left Right Case if (balance > 1 && key > node->left->key) { node->left =  leftRotate(node->left); return rightRotate(node); }   // Right Left Case if (balance < -1 && key < node->right->key) { node->right = rightRotate(node->right); return leftRotate(node); }   /* return the (unchanged) node pointer */ return node; }   // A utility function to print preorder traversal // of the tree. // The function also prints height of every node void preOrder(struct Node *root) { if(root != NULL) { printf("%d ", root->key); preOrder(root->left); preOrder(root->right); } }   /* Driver program to test above function*/ int main() { struct Node *root = NULL;   /* Constructing tree given in the above figure */ root = insert(root, 10); root = insert(root, 20); root = insert(root, 30); root = insert(root, 40); root = insert(root, 50); root = insert(root, 25);   /* The constructed AVL Tree would be 30 /  \ 20   40 /  \     \ 10  25    50 */   printf("Preorder traversal of the constructed AVL" " tree is \n"); preOrder(root);   return 0; } | | — |

Java

| // Java program for insertion in AVL Tree class Node { int key, height; Node left, right;   Node(int d) { key = d; height = 1; } }   class AVLTree {   Node root;   // A utility function to get the height of the tree int height(Node N) { if (N == null) return 0;   return N.height; }   // A utility function to get maximum of two integers int max(int a, int b) { return (a > b) ? a : b; }   // A utility function to right rotate subtree rooted with y // See the diagram given above. Node rightRotate(Node y) { Node x = y.left; Node T2 = x.right;   // Perform rotation x.right = y; y.left = T2;   // Update heights y.height = max(height(y.left), height(y.right)) + 1; x.height = max(height(x.left), height(x.right)) + 1;   // Return new root return x; }   // A utility function to left rotate subtree rooted with x // See the diagram given above. Node leftRotate(Node x) { Node y = x.right; Node T2 = y.left;   // Perform rotation y.left = x; x.right = T2;   //  Update heights x.height = max(height(x.left), height(x.right)) + 1; y.height = max(height(y.left), height(y.right)) + 1;   // Return new root return y; }   // Get Balance factor of node N int getBalance(Node N) { if (N == null) return 0;   return height(N.left) - height(N.right); }   Node insert(Node node, int key) {   /* 1.  Perform the normal BST insertion */ if (node == null) return (new Node(key));   if (key < node.key) node.left = insert(node.left, key); else if (key > node.key) node.right = insert(node.right, key); else // Duplicate keys not allowed return node;   /* 2. Update height of this ancestor node */ node.height = 1 + max(height(node.left), height(node.right));   /* 3. Get the balance factor of this ancestor node to check whether this node became unbalanced */ int balance = getBalance(node);   // If this node becomes unbalanced, then there // are 4 cases Left Left Case if (balance > 1 && key < node.left.key) return rightRotate(node);   // Right Right Case if (balance < -1 && key > node.right.key) return leftRotate(node);   // Left Right Case if (balance > 1 && key > node.left.key) { node.left = leftRotate(node.left); return rightRotate(node); }   // Right Left Case if (balance < -1 && key < node.right.key) { node.right = rightRotate(node.right); return leftRotate(node); }   /* return the (unchanged) node pointer */ return node; }   // A utility function to print preorder traversal // of the tree. // The function also prints height of every node void preOrder(Node node) { if (node != null) { System.out.print(node.key + " "); preOrder(node.left); preOrder(node.right); } }   public static void main(String[] args) { AVLTree tree = new AVLTree();   /* Constructing tree given in the above figure */ tree.root = tree.insert(tree.root, 10); tree.root = tree.insert(tree.root, 20); tree.root = tree.insert(tree.root, 30); tree.root = tree.insert(tree.root, 40); tree.root = tree.insert(tree.root, 50); tree.root = tree.insert(tree.root, 25);   /* The constructed AVL Tree would be 30 /  \ 20   40 /  \     \ 10  25    50 */ System.out.println("Preorder traversal" + " of constructed tree is : "); tree.preOrder(tree.root); } } // This code has been contributed by Mayank Jaiswal | | — |

Python3

| # Python code to insert a node in AVL tree   # Generic tree node class class TreeNode(object): def __init__(self, val): self.val = val self.left = None self.right = None self.height = 1   # AVL tree class which supports the # Insert operation class AVL_Tree(object):   # Recursive function to insert key in # subtree rooted with node and returns # new root of subtree. def insert(self, root, key):   # Step 1 - Perform normal BST if not root: return TreeNode(key) elif key < root.val: root.left = self.insert(root.left, key) else: root.right = self.insert(root.right, key)   # Step 2 - Update the height of the # ancestor node root.height = 1 + max(self.getHeight(root.left), self.getHeight(root.right))   # Step 3 - Get the balance factor balance = self.getBalance(root)   # Step 4 - If the node is unbalanced, # then try out the 4 cases # Case 1 - Left Left if balance > 1 and key < root.left.val: return self.rightRotate(root)   # Case 2 - Right Right if balance < -1 and key > root.right.val: return self.leftRotate(root)   # Case 3 - Left Right if balance > 1 and key > root.left.val: root.left = self.leftRotate(root.left) return self.rightRotate(root)   # Case 4 - Right Left if balance < -1 and key < root.right.val: root.right = self.rightRotate(root.right) return self.leftRotate(root)   return root   def leftRotate(self, z):   y = z.right T2 = y.left   # Perform rotation y.left = z z.right = T2   # Update heights z.height = 1 + max(self.getHeight(z.left), self.getHeight(z.right)) y.height = 1 + max(self.getHeight(y.left), self.getHeight(y.right))   # Return the new root return y   def rightRotate(self, z):   y = z.left T3 = y.right   # Perform rotation y.right = z z.left = T3   # Update heights z.height = 1 + max(self.getHeight(z.left), self.getHeight(z.right)) y.height = 1 + max(self.getHeight(y.left), self.getHeight(y.right))   # Return the new root return y   def getHeight(self, root): if not root: return 0   return root.height   def getBalance(self, root): if not root: return 0   return self.getHeight(root.left) - self.getHeight(root.right)   def preOrder(self, root):   if not root: return   print("{0} ".format(root.val), end="") self.preOrder(root.left) self.preOrder(root.right)     # Driver program to test above function myTree = AVL_Tree() root = None   root = myTree.insert(root, 10) root = myTree.insert(root, 20) root = myTree.insert(root, 30) root = myTree.insert(root, 40) root = myTree.insert(root, 50) root = myTree.insert(root, 25)   """The constructed AVL Tree would be 30 /  \ 20   40 /  \     \ 10  25    50"""   # Preorder Traversal print("Preorder traversal of the", "constructed AVL tree is") myTree.preOrder(root) print()   # This code is contributed by Ajitesh Pathak | | — |

C#

| // C# program for insertion in AVL Tree using System;   class Node { public int key, height; public Node left, right;   public Node(int d) { key = d; height = 1; } }   public class AVLTree {   Node root;   // A utility function to get // the height of the tree int height(Node N) { if (N == null) return 0;   return N.height; }   // A utility function to get // maximum of two integers int max(int a, int b) { return (a > b) ? a : b; }   // A utility function to right // rotate subtree rooted with y // See the diagram given above. Node rightRotate(Node y) { Node x = y.left; Node T2 = x.right;   // Perform rotation x.right = y; y.left = T2;   // Update heights y.height = max(height(y.left), height(y.right)) + 1; x.height = max(height(x.left), height(x.right)) + 1;   // Return new root return x; }   // A utility function to left // rotate subtree rooted with x // See the diagram given above. Node leftRotate(Node x) { Node y = x.right; Node T2 = y.left;   // Perform rotation y.left = x; x.right = T2;   // Update heights x.height = max(height(x.left), height(x.right)) + 1; y.height = max(height(y.left), height(y.right)) + 1;   // Return new root return y; }   // Get Balance factor of node N int getBalance(Node N) { if (N == null) return 0;   return height(N.left) - height(N.right); }   Node insert(Node node, int key) {   /* 1. Perform the normal BST insertion */ if (node == null) return (new Node(key));   if (key < node.key) node.left = insert(node.left, key); else if (key > node.key) node.right = insert(node.right, key); else // Duplicate keys not allowed return node;   /* 2. Update height of this ancestor node */ node.height = 1 + max(height(node.left), height(node.right));   /* 3. Get the balance factor of this ancestor node to check whether this node became unbalanced */ int balance = getBalance(node);   // If this node becomes unbalanced, then there // are 4 cases Left Left Case if (balance > 1 && key < node.left.key) return rightRotate(node);   // Right Right Case if (balance < -1 && key > node.right.key) return leftRotate(node);   // Left Right Case if (balance > 1 && key > node.left.key) { node.left = leftRotate(node.left); return rightRotate(node); }   // Right Left Case if (balance < -1 && key < node.right.key) { node.right = rightRotate(node.right); return leftRotate(node); }   /* return the (unchanged) node pointer */ return node; }   // A utility function to print preorder traversal // of the tree. // The function also prints height of every node void preOrder(Node node) { if (node != null) { Console.Write(node.key + " "); preOrder(node.left); preOrder(node.right); } }   // Driver code public static void Main(String[] args) { AVLTree tree = new AVLTree();   /* Constructing tree given in the above figure */ tree.root = tree.insert(tree.root, 10); tree.root = tree.insert(tree.root, 20); tree.root = tree.insert(tree.root, 30); tree.root = tree.insert(tree.root, 40); tree.root = tree.insert(tree.root, 50); tree.root = tree.insert(tree.root, 25);   /* The constructed AVL Tree would be 30 / \ 20 40 / \ \ 10 25 50 */ Console.Write("Preorder traversal" + " of constructed tree is : "); tree.preOrder(tree.root); } }   // This code has been contributed // by PrinciRaj1992 | | — |

Javascript

| <script>   // JavaScript program for insertion in AVL Tree class Node { constructor(d) { this.key = d; this.height = 1; this.left = null; this.right = null; } }   class AVLTree { constructor() { this.root = null; }   // A utility function to get // the height of the tree height(N) { if (N == null) return 0;   return N.height; }   // A utility function to get // maximum of two integers max(a, b) { return a > b ? a : b; }   // A utility function to right // rotate subtree rooted with y // See the diagram given above. rightRotate(y) { var x = y.left; var T2 = x.right;   // Perform rotation x.right = y; y.left = T2;   // Update heights y.height = this.max(this.height(y.left), this.height(y.right)) + 1; x.height = this.max(this.height(x.left), this.height(x.right)) + 1;   // Return new root return x; }   // A utility function to left // rotate subtree rooted with x // See the diagram given above. leftRotate(x) { var y = x.right; var T2 = y.left;   // Perform rotation y.left = x; x.right = T2;   // Update heights x.height = this.max(this.height(x.left), this.height(x.right)) + 1; y.height = this.max(this.height(y.left), this.height(y.right)) + 1;   // Return new root return y; }   // Get Balance factor of node N getBalance(N) { if (N == null) return 0;   return this.height(N.left) - this.height(N.right); }   insert(node, key) { /* 1. Perform the normal BST insertion */ if (node == null) return new Node(key);   if (key < node.key) node.left = this.insert(node.left, key); else if (key > node.key) node.right = this.insert(node.right, key); // Duplicate keys not allowed else return node;   /* 2. Update height of this ancestor node */ node.height = 1 + this.max(this.height(node.left), this.height(node.right));   /* 3. Get the balance factor of this ancestor node to check whether this node became unbalanced */ var balance = this.getBalance(node);   // If this node becomes unbalanced, then there // are 4 cases Left Left Case if (balance > 1 && key < node.left.key) return this.rightRotate(node);   // Right Right Case if (balance < -1 && key > node.right.key) return this.leftRotate(node);   // Left Right Case if (balance > 1 && key > node.left.key) { node.left = this.leftRotate(node.left); return this.rightRotate(node); }   // Right Left Case if (balance < -1 && key < node.right.key) { node.right = this.rightRotate(node.right); return this.leftRotate(node); }   /* return the (unchanged) node pointer */ return node; }   // A utility function to print preorder traversal // of the tree. // The function also prints height of every node preOrder(node) { if (node != null) { document.write(node.key + " "); this.preOrder(node.left); this.preOrder(node.right); } } } // Driver code var tree = new AVLTree();   /* Constructing tree given in the above figure */ tree.root = tree.insert(tree.root, 10); tree.root = tree.insert(tree.root, 20); tree.root = tree.insert(tree.root, 30); tree.root = tree.insert(tree.root, 40); tree.root = tree.insert(tree.root, 50); tree.root = tree.insert(tree.root, 25);   /* The constructed AVL Tree would be 30 / \ 20 40 / \   \ 10 25  50 */ document.write( "Preorder traversal of the " + "constructed AVL tree is <br>" ); tree.preOrder(tree.root);   </script> | | — |

Output

Preorder traversal of the constructed AVL tree is 
30 20 10 25 40 50 

Complexity Analysis

Time Complexity: O(log(n)), For Insertion
Auxiliary Space: O(1)

The rotation operations (left and right rotate) take constant time as only a few pointers are being changed there. Updating the height and getting the balance factor also takes constant time. So the time complexity of the AVL insert remains the same as the BST insert which is O(h) where h is the height of the tree. Since the AVL tree is balanced, the height is O(Logn). So time complexity of AVL insert is O(Logn).

Comparison with Red Black Tree:

The AVL tree and other self-balancing search trees like Red Black are useful to get all basic operations done in O(log n) time. The AVL trees are more balanced compared to Red-Black Trees, but they may cause more rotations during insertion and deletion. So if your application involves many frequent insertions and deletions, then Red Black trees should be preferred. And if the insertions and deletions are less frequent and search is the more frequent operation, then the AVL tree should be preferred over Red Black Tree.

Following is the post for deletion in AVL Tree:
AVL Tree | Set 2 (Deletion)

Previous

[What is AVL Tree

AVL Tree meaning](https://www.geeksforgeeks.org/what-is-avl-tree-avl-tree-meaning/?ref=previous_article)

Next

Insertion, Searching and Deletion in AVL trees containing a parent node pointer

---

Deletion in an AVL Tree =======================

  We have discussed AVL insertion in the previous post. In this post, we will follow a similar approach for deletion.

Steps to follow for deletion. 
To make sure that the given tree remains AVL after every deletion, we must augment the standard BST delete operation to perform some re-balancing. Following are two basic operations that can be performed to re-balance a BST without violating the BST property (keys(left) < key(root) < keys(right)). 

1. Left Rotation
2. Right Rotation

T1, T2 and T3 are subtrees of the tree rooted with y (on left side)
or x (on right side)
                y                               x
               / \     Right Rotation          /  \
              x   T3   – - – - – - – >        T1   y
             / \       < - - - - - - -            / \
            T1  T2     Left Rotation            T2  T3
Keys in both of the above trees follow the following order
      keys(T1) < key(x) < keys(T2) < key(y) < keys(T3)
So BST property is not violated anywhere.

Let w be the node to be deleted 

1. Perform standard BST delete for w.
2. Starting from w, travel up and find the first unbalanced node. Let z be the first unbalanced node, y be the larger height child of z, and x be the larger height child of y. Note that the definitions of x and y are different from insertion here.
3. Re-balance the tree by performing appropriate rotations on the subtree rooted with z. There can be 4 possible cases that needs to be handled as x, y and z can be arranged in 4 ways. Following are the possible 4 arrangements:
   1. y is left child of z and x is left child of y (Left Left Case)
   2. y is left child of z and x is right child of y (Left Right Case)
   3. y is right child of z and x is right child of y (Right Right Case)
   4. y is right child of z and x is left child of y (Right Left Case)

Like insertion, following are the operations to be performed in above mentioned 4 cases. Note that, unlike insertion, fixing the node z won’t fix the complete AVL tree. After fixing z, we may have to fix ancestors of z as well (See this video lecture for proof)

a) Left Left Case 

T1, T2, T3 and T4 are subtrees.
         z                                      y 
        / \                                   /   \
       y   T4      Right Rotate (z)          x      z
      / \          - - - - - - - - ->      /  \    /  \ 
     x   T3                               T1  T2  T3  T4
    / \
  T1   T2

b) Left Right Case 

     z                               z                           x
    / \                            /   \                        /  \ 
   y   T4  Left Rotate (y)        x    T4  Right Rotate(z)    y      z
  / \      - - - - - - - - ->    /  \      - - - - - - - ->  / \    / \
T1   x                          y    T3                    T1  T2 T3  T4
    / \                        / \
  T2   T3                    T1   T2

c) Right Right Case 

  z                                y
 /  \                            /   \ 
T1   y     Left Rotate(z)       z      x
    /  \   - - - - - - - ->    / \    / \
   T2   x                     T1  T2 T3  T4
       / \
     T3  T4

d) Right Left Case 

   z                            z                            x
  / \                          / \                          /  \ 
T1   y   Right Rotate (y)    T1   x      Left Rotate(z)   z      y
    / \  - - - - - - - - ->     /  \   - - - - - - - ->  / \    / \
   x   T4                      T2   y                  T1  T2  T3  T4
  / \                              /  \
T2   T3                           T3   T4

Unlike insertion, in deletion, after we perform a rotation at z, we may have to perform a rotation at ancestors of z. Thus, we must continue to trace the path until we reach the root.

Example:  

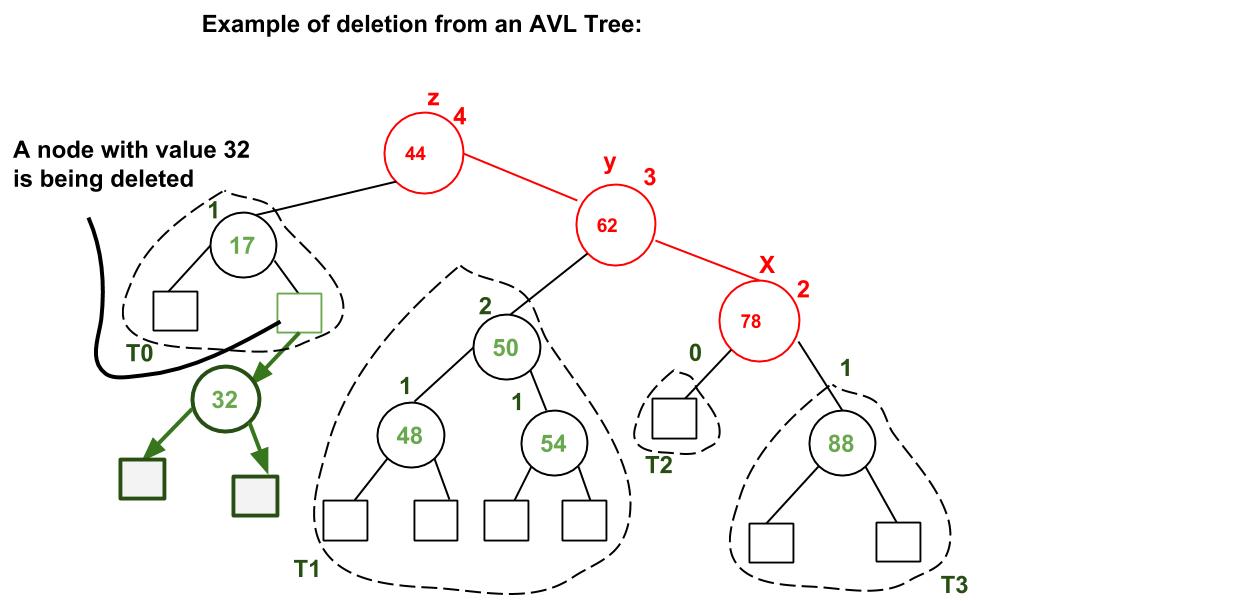
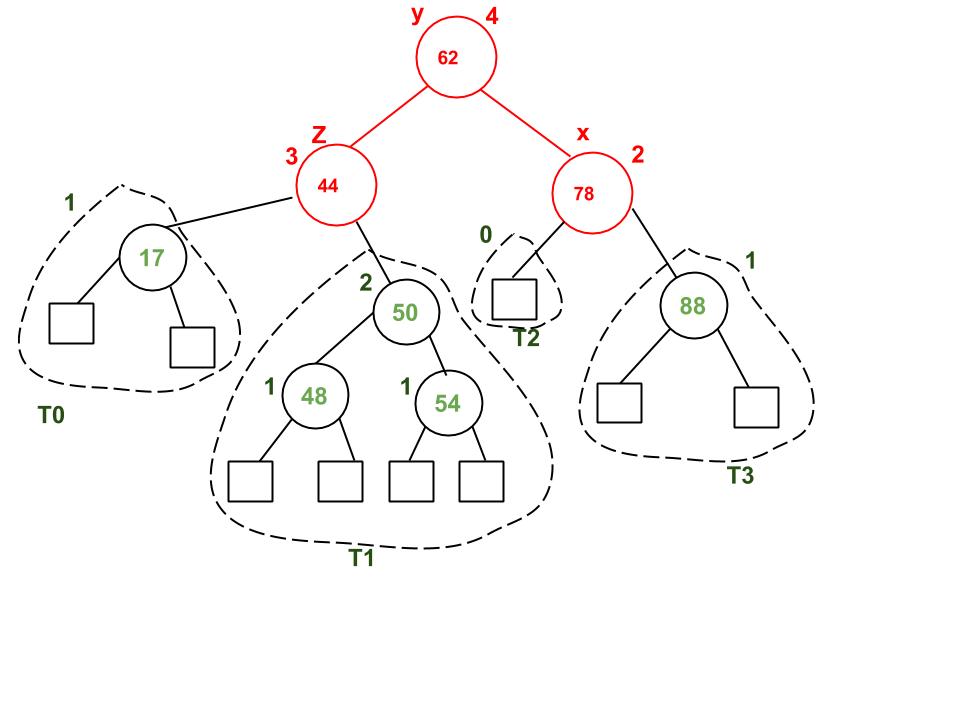
A node with value 32 is being deleted. After deleting 32, we travel up and find the first unbalanced node which is 44. We mark it as z, its higher height child as y which is 62, and y’s higher height child as x which could be either 78 or 50 as both are of same height. We have considered 78. Now the case is Right Right, so we perform left rotation.

Recommended Practice AVL Tree Deletion

Try It!

C implementation 
Following is the C implementation for AVL Tree Deletion. The following C implementation uses the recursive BST delete as basis. In the recursive BST delete, after deletion, we get pointers to all ancestors one by one in bottom up manner. So we don’t need parent pointer to travel up. The recursive code itself travels up and visits all the ancestors of the deleted node. 

1. Perform the normal BST deletion.
2. The current node must be one of the ancestors of the deleted node. Update the height of the current node.
3. Get the balance factor (left subtree height – right subtree height) of the current node.
4. If balance factor is greater than 1, then the current node is unbalanced and we are either in Left Left case or Left Right case. To check whether it is Left Left case or Left Right case, get the balance factor of left subtree. If balance factor of the left subtree is greater than or equal to 0, then it is Left Left case, else Left Right case.
5. If balance factor is less than -1, then the current node is unbalanced and we are either in Right Right case or Right Left case. To check whether it is Right Right case or Right Left case, get the balance factor of right subtree. If the balance factor of the right subtree is smaller than or equal to 0, then it is Right Right case, else Right Left case.

C++

| // C++ program to delete a node from AVL Tree #include<bits/stdc++.h> using namespace std;   // An AVL tree node class Node { public: int key; Node *left; Node *right; int height; };   // A utility function to get maximum // of two integers int max(int a, int b);   // A utility function to get height // of the tree int height(Node *N) { if (N == NULL) return 0; return N->height; }   // A utility function to get maximum // of two integers int max(int a, int b) { return (a > b)? a : b; }   /* Helper function that allocates a new node with the given key and NULL left and right pointers. */ Node* newNode(int key) { Node* node = new Node(); node->key = key; node->left = NULL; node->right = NULL; node->height = 1; // new node is initially // added at leaf return(node); }   // A utility function to right // rotate subtree rooted with y // See the diagram given above. Node *rightRotate(Node *y) { Node *x = y->left; Node *T2 = x->right;   // Perform rotation x->right = y; y->left = T2;   // Update heights y->height = max(height(y->left), height(y->right)) + 1; x->height = max(height(x->left), height(x->right)) + 1;   // Return new root return x; }   // A utility function to left // rotate subtree rooted with x // See the diagram given above. Node *leftRotate(Node *x) { Node *y = x->right; Node *T2 = y->left;   // Perform rotation y->left = x; x->right = T2;   // Update heights x->height = max(height(x->left), height(x->right)) + 1; y->height = max(height(y->left), height(y->right)) + 1;   // Return new root return y; }   // Get Balance factor of node N int getBalance(Node *N) { if (N == NULL) return 0; return height(N->left) - height(N->right); }   Node* insert(Node* node, int key) { /* 1. Perform the normal BST rotation */ if (node == NULL) return(newNode(key));   if (key < node->key) node->left = insert(node->left, key); else if (key > node->key) node->right = insert(node->right, key); else // Equal keys not allowed return node;   /* 2. Update height of this ancestor node */ node->height = 1 + max(height(node->left), height(node->right));   /* 3. Get the balance factor of this ancestor node to check whether this node became unbalanced */ int balance = getBalance(node);   // If this node becomes unbalanced, // then there are 4 cases   // Left Left Case if (balance > 1 && key < node->left->key) return rightRotate(node);   // Right Right Case if (balance < -1 && key > node->right->key) return leftRotate(node);   // Left Right Case if (balance > 1 && key > node->left->key) { node->left = leftRotate(node->left); return rightRotate(node); }   // Right Left Case if (balance < -1 && key < node->right->key) { node->right = rightRotate(node->right); return leftRotate(node); }   /* return the (unchanged) node pointer */ return node; }   /* Given a non-empty binary search tree, return the node with minimum key value found in that tree. Note that the entire tree does not need to be searched. */ Node * minValueNode(Node* node) { Node* current = node;   /* loop down to find the leftmost leaf */ while (current->left != NULL) current = current->left;   return current; }   // Recursive function to delete a node // with given key from subtree with // given root. It returns root of the // modified subtree. Node* deleteNode(Node* root, int key) {   // STEP 1: PERFORM STANDARD BST DELETE if (root == NULL) return root;   // If the key to be deleted is smaller // than the root's key, then it lies // in left subtree if ( key < root->key ) root->left = deleteNode(root->left, key);   // If the key to be deleted is greater // than the root's key, then it lies // in right subtree else if( key > root->key ) root->right = deleteNode(root->right, key);   // if key is same as root's key, then // This is the node to be deleted else { // node with only one child or no child if( (root->left == NULL) || (root->right == NULL) ) { Node *temp = root->left ? root->left : root->right;   // No child case if (temp == NULL) { temp = root; root = NULL; } else // One child case *root = *temp; // Copy the contents of // the non-empty child free(temp); } else { // node with two children: Get the inorder // successor (smallest in the right subtree) Node* temp = minValueNode(root->right);   // Copy the inorder successor's // data to this node root->key = temp->key;   // Delete the inorder successor root->right = deleteNode(root->right, temp->key); } }   // If the tree had only one node // then return if (root == NULL) return root;   // STEP 2: UPDATE HEIGHT OF THE CURRENT NODE root->height = 1 + max(height(root->left), height(root->right));   // STEP 3: GET THE BALANCE FACTOR OF // THIS NODE (to check whether this // node became unbalanced) int balance = getBalance(root);   // If this node becomes unbalanced, // then there are 4 cases   // Left Left Case if (balance > 1 && getBalance(root->left) >= 0) return rightRotate(root);   // Left Right Case if (balance > 1 && getBalance(root->left) < 0) { root->left = leftRotate(root->left); return rightRotate(root); }   // Right Right Case if (balance < -1 && getBalance(root->right) <= 0) return leftRotate(root);   // Right Left Case if (balance < -1 && getBalance(root->right) > 0) { root->right = rightRotate(root->right); return leftRotate(root); }   return root; }   // A utility function to print preorder // traversal of the tree. // The function also prints height // of every node void preOrder(Node *root) { if(root != NULL) { cout << root->key << " "; preOrder(root->left); preOrder(root->right); } }   // Driver Code int main() { Node *root = NULL;   /* Constructing tree given in the above figure */ root = insert(root, 9); root = insert(root, 5); root = insert(root, 10); root = insert(root, 0); root = insert(root, 6); root = insert(root, 11); root = insert(root, -1); root = insert(root, 1); root = insert(root, 2);   /* The constructed AVL Tree would be 9 / \ 1 10 / \ \ 0 5 11 / / \ -1 2 6 */   cout << "Preorder traversal of the " "constructed AVL tree is \n"; preOrder(root);   root = deleteNode(root, 10);   /* The AVL Tree after deletion of 10 1 / \ 0 9 / / \ -1 5     11 / \ 2 6 */   cout << "\nPreorder traversal after" << " deletion of 10 \n"; preOrder(root);   return 0; }   // This code is contributed by rathbhupendra | | — |

C

| // C program to delete a node from AVL Tree #include<stdio.h> #include<stdlib.h>   // An AVL tree node struct Node { int key; struct Node *left; struct Node *right; int height; };   // A utility function to get maximum of two integers int max(int a, int b);   // A utility function to get height of the tree int height(struct Node *N) { if (N == NULL) return 0; return N->height; }   // A utility function to get maximum of two integers int max(int a, int b) { return (a > b)? a : b; }   /* Helper function that allocates a new node with the given key and NULL left and right pointers. */ struct Node* newNode(int key) { struct Node* node = (struct Node*) malloc(sizeof(struct Node)); node->key   = key; node->left   = NULL; node->right  = NULL; node->height = 1; // new node is initially added at leaf return(node); }   // A utility function to right rotate subtree rooted with y // See the diagram given above. struct Node *rightRotate(struct Node *y) { struct Node *x = y->left; struct Node *T2 = x->right;   // Perform rotation x->right = y; y->left = T2;   // Update heights y->height = max(height(y->left), height(y->right))+1; x->height = max(height(x->left), height(x->right))+1;   // Return new root return x; }   // A utility function to left rotate subtree rooted with x // See the diagram given above. struct Node *leftRotate(struct Node *x) { struct Node *y = x->right; struct Node *T2 = y->left;   // Perform rotation y->left = x; x->right = T2;   //  Update heights x->height = max(height(x->left), height(x->right))+1; y->height = max(height(y->left), height(y->right))+1;   // Return new root return y; }   // Get Balance factor of node N int getBalance(struct Node *N) { if (N == NULL) return 0; return height(N->left) - height(N->right); }   struct Node* insert(struct Node* node, int key) { /* 1.  Perform the normal BST rotation */ if (node == NULL) return(newNode(key));   if (key < node->key) node->left  = insert(node->left, key); else if (key > node->key) node->right = insert(node->right, key); else // Equal keys not allowed return node;   /* 2. Update height of this ancestor node */ node->height = 1 + max(height(node->left), height(node->right));   /* 3. Get the balance factor of this ancestor node to check whether this node became unbalanced */ int balance = getBalance(node);   // If this node becomes unbalanced, then there are 4 cases   // Left Left Case if (balance > 1 && key < node->left->key) return rightRotate(node);   // Right Right Case if (balance < -1 && key > node->right->key) return leftRotate(node);   // Left Right Case if (balance > 1 && key > node->left->key) { node->left =  leftRotate(node->left); return rightRotate(node); }   // Right Left Case if (balance < -1 && key < node->right->key) { node->right = rightRotate(node->right); return leftRotate(node); }   /* return the (unchanged) node pointer */ return node; }   /* Given a non-empty binary search tree, return the node with minimum key value found in that tree. Note that the entire tree does not need to be searched. */ struct Node * minValueNode(struct Node* node) { struct Node* current = node;   /* loop down to find the leftmost leaf */ while (current->left != NULL) current = current->left;   return current; }   // Recursive function to delete a node with given key // from subtree with given root. It returns root of // the modified subtree. struct Node* deleteNode(struct Node* root, int key) { // STEP 1: PERFORM STANDARD BST DELETE   if (root == NULL) return root;   // If the key to be deleted is smaller than the // root's key, then it lies in left subtree if ( key < root->key ) root->left = deleteNode(root->left, key);   // If the key to be deleted is greater than the // root's key, then it lies in right subtree else if( key > root->key ) root->right = deleteNode(root->right, key);   // if key is same as root's key, then This is // the node to be deleted else { // node with only one child or no child if( (root->left == NULL) || (root->right == NULL) ) { struct Node *temp = root->left ? root->left : root->right;   // No child case if (temp == NULL) { temp = root; root = NULL; } else // One child case *root = *temp; // Copy the contents of // the non-empty child free(temp); } else { // node with two children: Get the inorder // successor (smallest in the right subtree) struct Node* temp = minValueNode(root->right);   // Copy the inorder successor's data to this node root->key = temp->key;   // Delete the inorder successor root->right = deleteNode(root->right, temp->key); } }   // If the tree had only one node then return if (root == NULL) return root;   // STEP 2: UPDATE HEIGHT OF THE CURRENT NODE root->height = 1 + max(height(root->left), height(root->right));   // STEP 3: GET THE BALANCE FACTOR OF THIS NODE (to // check whether this node became unbalanced) int balance = getBalance(root);   // If this node becomes unbalanced, then there are 4 cases   // Left Left Case if (balance > 1 && getBalance(root->left) >= 0) return rightRotate(root);   // Left Right Case if (balance > 1 && getBalance(root->left) < 0) { root->left =  leftRotate(root->left); return rightRotate(root); }   // Right Right Case if (balance < -1 && getBalance(root->right) <= 0) return leftRotate(root);   // Right Left Case if (balance < -1 && getBalance(root->right) > 0) { root->right = rightRotate(root->right); return leftRotate(root); }   return root; }   // A utility function to print preorder traversal of // the tree. // The function also prints height of every node void preOrder(struct Node *root) { if(root != NULL) { printf("%d ", root->key); preOrder(root->left); preOrder(root->right); } }   /* Driver program to test above function*/ int main() { struct Node *root = NULL;   /* Constructing tree given in the above figure */ root = insert(root, 9); root = insert(root, 5); root = insert(root, 10); root = insert(root, 0); root = insert(root, 6); root = insert(root, 11); root = insert(root, -1); root = insert(root, 1); root = insert(root, 2);   /* The constructed AVL Tree would be 9 /  \ 1    10 /  \     \ 0    5     11 /    /  \ -1   2    6 */   printf("Preorder traversal of the constructed AVL " "tree is \n"); preOrder(root);   root = deleteNode(root, 10);   /* The AVL Tree after deletion of 10 1 /  \ 0    9 /     /  \ -1    5     11 /  \ 2    6 */   printf("\nPreorder traversal after deletion of 10 \n"); preOrder(root);   return 0; } | | — |

Java

| // Java program for deletion in AVL Tree   class Node { int key, height; Node left, right;   Node(int d) { key = d; height = 1; } }   class AVLTree { Node root;   // A utility function to get height of the tree int height(Node N) { if (N == null) return 0; return N.height; }   // A utility function to get maximum of two integers int max(int a, int b) { return (a > b) ? a : b; }   // A utility function to right rotate subtree rooted with y // See the diagram given above. Node rightRotate(Node y) { Node x = y.left; Node T2 = x.right;   // Perform rotation x.right = y; y.left = T2;   // Update heights y.height = max(height(y.left), height(y.right)) + 1; x.height = max(height(x.left), height(x.right)) + 1;   // Return new root return x; }   // A utility function to left rotate subtree rooted with x // See the diagram given above. Node leftRotate(Node x) { Node y = x.right; Node T2 = y.left;   // Perform rotation y.left = x; x.right = T2;   // Update heights x.height = max(height(x.left), height(x.right)) + 1; y.height = max(height(y.left), height(y.right)) + 1;   // Return new root return y; }   // Get Balance factor of node N int getBalance(Node N) { if (N == null) return 0; return height(N.left) - height(N.right); }   Node insert(Node node, int key) { /* 1. Perform the normal BST rotation */ if (node == null) return (new Node(key));   if (key < node.key) node.left = insert(node.left, key); else if (key > node.key) node.right = insert(node.right, key); else // Equal keys not allowed return node;   /* 2. Update height of this ancestor node */ node.height = 1 + max(height(node.left), height(node.right));   /* 3. Get the balance factor of this ancestor node to check whether this node became Wunbalanced */ int balance = getBalance(node);   // If this node becomes unbalanced, then // there are 4 cases Left Left Case if (balance > 1 && key < node.left.key) return rightRotate(node);   // Right Right Case if (balance < -1 && key > node.right.key) return leftRotate(node);   // Left Right Case if (balance > 1 && key > node.left.key) { node.left = leftRotate(node.left); return rightRotate(node); }   // Right Left Case if (balance < -1 && key < node.right.key) { node.right = rightRotate(node.right); return leftRotate(node); }   /* return the (unchanged) node pointer */ return node; }   /* Given a non-empty binary search tree, return the node with minimum key value found in that tree. Note that the entire tree does not need to be searched. */ Node minValueNode(Node node) { Node current = node;   /* loop down to find the leftmost leaf */ while (current.left != null) current = current.left;   return current; }   Node deleteNode(Node root, int key) { // STEP 1: PERFORM STANDARD BST DELETE if (root == null) return root;   // If the key to be deleted is smaller than // the root's key, then it lies in left subtree if (key < root.key) root.left = deleteNode(root.left, key);   // If the key to be deleted is greater than the // root's key, then it lies in right subtree else if (key > root.key) root.right = deleteNode(root.right, key);   // if key is same as root's key, then this is the node // to be deleted else {   // node with only one child or no child if ((root.left == null) || (root.right == null)) { Node temp = null; if (temp == root.left) temp = root.right; else temp = root.left;   // No child case if (temp == null) { temp = root; root = null; } else // One child case root = temp; // Copy the contents of // the non-empty child } else {   // node with two children: Get the inorder // successor (smallest in the right subtree) Node temp = minValueNode(root.right);   // Copy the inorder successor's data to this node root.key = temp.key;   // Delete the inorder successor root.right = deleteNode(root.right, temp.key); } }   // If the tree had only one node then return if (root == null) return root;   // STEP 2: UPDATE HEIGHT OF THE CURRENT NODE root.height = max(height(root.left), height(root.right)) + 1;   // STEP 3: GET THE BALANCE FACTOR OF THIS NODE (to check whether // this node became unbalanced) int balance = getBalance(root);   // If this node becomes unbalanced, then there are 4 cases // Left Left Case if (balance > 1 && getBalance(root.left) >= 0) return rightRotate(root);   // Left Right Case if (balance > 1 && getBalance(root.left) < 0) { root.left = leftRotate(root.left); return rightRotate(root); }   // Right Right Case if (balance < -1 && getBalance(root.right) <= 0) return leftRotate(root);   // Right Left Case if (balance < -1 && getBalance(root.right) > 0) { root.right = rightRotate(root.right); return leftRotate(root); }   return root; }   // A utility function to print preorder traversal of // the tree. The function also prints height of every // node void preOrder(Node node) { if (node != null) { System.out.print(node.key + " "); preOrder(node.left); preOrder(node.right); } }   public static void main(String[] args) { AVLTree tree = new AVLTree();   /* Constructing tree given in the above figure */ tree.root = tree.insert(tree.root, 9); tree.root = tree.insert(tree.root, 5); tree.root = tree.insert(tree.root, 10); tree.root = tree.insert(tree.root, 0); tree.root = tree.insert(tree.root, 6); tree.root = tree.insert(tree.root, 11); tree.root = tree.insert(tree.root, -1); tree.root = tree.insert(tree.root, 1); tree.root = tree.insert(tree.root, 2);   /* The constructed AVL Tree would be 9 / \ 1 10 / \ \ 0 5 11 / / \ -1 2 6 */ System.out.println("Preorder traversal of "+ "constructed tree is : "); tree.preOrder(tree.root);   tree.root = tree.deleteNode(tree.root, 10);   /* The AVL Tree after deletion of 10 1 / \ 0 9 /     / \ -1 5 11 / \ 2 6 */ System.out.println(""); System.out.println("Preorder traversal after "+ "deletion of 10 :"); tree.preOrder(tree.root); } }   // This code has been contributed by Mayank Jaiswal | | — |

Python3

| # Python code to delete a node in AVL tree # Generic tree node class class TreeNode(object): def __init__(self, val): self.val = val self.left = None self.right = None self.height = 1   # AVL tree class which supports insertion, # deletion operations class AVL_Tree(object):   def insert(self, root, key):   # Step 1 - Perform normal BST if not root: return TreeNode(key) elif key < root.val: root.left = self.insert(root.left, key) else: root.right = self.insert(root.right, key)   # Step 2 - Update the height of the # ancestor node root.height = 1 + max(self.getHeight(root.left), self.getHeight(root.right))   # Step 3 - Get the balance factor balance = self.getBalance(root)   # Step 4 - If the node is unbalanced, # then try out the 4 cases # Case 1 - Left Left if balance > 1 and key < root.left.val: return self.rightRotate(root)   # Case 2 - Right Right if balance < -1 and key > root.right.val: return self.leftRotate(root)   # Case 3 - Left Right if balance > 1 and key > root.left.val: root.left = self.leftRotate(root.left) return self.rightRotate(root)   # Case 4 - Right Left if balance < -1 and key < root.right.val: root.right = self.rightRotate(root.right) return self.leftRotate(root)   return root   # Recursive function to delete a node with # given key from subtree with given root. # It returns root of the modified subtree. def delete(self, root, key):   # Step 1 - Perform standard BST delete if not root: return root   elif key < root.val: root.left = self.delete(root.left, key)   elif key > root.val: root.right = self.delete(root.right, key)   else: if root.left is None: temp = root.right root = None return temp   elif root.right is None: temp = root.left root = None return temp   temp = self.getMinValueNode(root.right) root.val = temp.val root.right = self.delete(root.right, temp.val)   # If the tree has only one node, # simply return it if root is None: return root   # Step 2 - Update the height of the # ancestor node root.height = 1 + max(self.getHeight(root.left), self.getHeight(root.right))   # Step 3 - Get the balance factor balance = self.getBalance(root)   # Step 4 - If the node is unbalanced, # then try out the 4 cases # Case 1 - Left Left if balance > 1 and self.getBalance(root.left) >= 0: return self.rightRotate(root)   # Case 2 - Right Right if balance < -1 and self.getBalance(root.right) <= 0: return self.leftRotate(root)   # Case 3 - Left Right if balance > 1 and self.getBalance(root.left) < 0: root.left = self.leftRotate(root.left) return self.rightRotate(root)   # Case 4 - Right Left if balance < -1 and self.getBalance(root.right) > 0: root.right = self.rightRotate(root.right) return self.leftRotate(root)   return root   def leftRotate(self, z):   y = z.right T2 = y.left   # Perform rotation y.left = z z.right = T2   # Update heights z.height = 1 + max(self.getHeight(z.left), self.getHeight(z.right)) y.height = 1 + max(self.getHeight(y.left), self.getHeight(y.right))   # Return the new root return y   def rightRotate(self, z):   y = z.left T3 = y.right   # Perform rotation y.right = z z.left = T3   # Update heights z.height = 1 + max(self.getHeight(z.left), self.getHeight(z.right)) y.height = 1 + max(self.getHeight(y.left), self.getHeight(y.right))   # Return the new root return y   def getHeight(self, root): if not root: return 0   return root.height   def getBalance(self, root): if not root: return 0   return self.getHeight(root.left) - self.getHeight(root.right)   def getMinValueNode(self, root): if root is None or root.left is None: return root   return self.getMinValueNode(root.left)   def preOrder(self, root):   if not root: return   print("{0} ".format(root.val), end="") self.preOrder(root.left) self.preOrder(root.right)     myTree = AVL_Tree() root = None nums = [9, 5, 10, 0, 6, 11, -1, 1, 2]   for num in nums: root = myTree.insert(root, num)   # Preorder Traversal print("Preorder Traversal after insertion -") myTree.preOrder(root) print()   # Delete key = 10 root = myTree.delete(root, key)   # Preorder Traversal print("Preorder Traversal after deletion -") myTree.preOrder(root) print()   # This code is contributed by Ajitesh Pathak | | — |

C#

| // C# program for deletion in AVL Tree using System;   public class Node { public int key, height; public Node left, right;   public Node(int d) { key = d; height = 1; } }   public class AVLTree { Node root;   // A utility function to get height of the tree int height(Node N) { if (N == null) return 0; return N.height; }   // A utility function to // get maximum of two integers int max(int a, int b) { return (a > b) ? a : b; }   // A utility function to right // rotate subtree rooted with y // See the diagram given above. Node rightRotate(Node y) { Node x = y.left; Node T2 = x.right;   // Perform rotation x.right = y; y.left = T2;   // Update heights y.height = max(height(y.left), height(y.right)) + 1; x.height = max(height(x.left), height(x.right)) + 1;   // Return new root return x; }   // A utility function to left // rotate subtree rooted with x // See the diagram given above. Node leftRotate(Node x) { Node y = x.right; Node T2 = y.left;   // Perform rotation y.left = x; x.right = T2;   // Update heights x.height = max(height(x.left), height(x.right)) + 1; y.height = max(height(y.left), height(y.right)) + 1;   // Return new root return y; }   // Get Balance factor of node N int getBalance(Node N) { if (N == null) return 0; return height(N.left) - height(N.right); }   Node insert(Node node, int key) { /* 1. Perform the normal BST rotation */ if (node == null) return (new Node(key));   if (key < node.key) node.left = insert(node.left, key); else if (key > node.key) node.right = insert(node.right, key); else // Equal keys not allowed return node;   /* 2. Update height of this ancestor node */ node.height = 1 + max(height(node.left), height(node.right));   /* 3. Get the balance factor of this ancestor node to check whether this node became Wunbalanced */ int balance = getBalance(node);   // If this node becomes unbalanced, then // there are 4 cases Left Left Case if (balance > 1 && key < node.left.key) return rightRotate(node);   // Right Right Case if (balance < -1 && key > node.right.key) return leftRotate(node);   // Left Right Case if (balance > 1 && key > node.left.key) { node.left = leftRotate(node.left); return rightRotate(node); }   // Right Left Case if (balance < -1 && key < node.right.key) { node.right = rightRotate(node.right); return leftRotate(node); }   /* return the (unchanged) node pointer */ return node; }   /* Given a non-empty binary search tree, return the node with minimum key value found in that tree. Note that the entire tree does not need to be searched. */ Node minValueNode(Node node) { Node current = node;   /* loop down to find the leftmost leaf */ while (current.left != null) current = current.left;   return current; }   Node deleteNode(Node root, int key) { // STEP 1: PERFORM STANDARD BST DELETE if (root == null) return root;   // If the key to be deleted is smaller than // the root's key, then it lies in left subtree if (key < root.key) root.left = deleteNode(root.left, key);   // If the key to be deleted is greater than the // root's key, then it lies in right subtree else if (key > root.key) root.right = deleteNode(root.right, key);   // if key is same as root's key, then this is the node // to be deleted else {   // node with only one child or no child if ((root.left == null) || (root.right == null)) { Node temp = null; if (temp == root.left) temp = root.right; else temp = root.left;   // No child case if (temp == null) { temp = root; root = null; } else // One child case root = temp; // Copy the contents of // the non-empty child } else {   // node with two children: Get the inorder // successor (smallest in the right subtree) Node temp = minValueNode(root.right);   // Copy the inorder successor's data to this node root.key = temp.key;   // Delete the inorder successor root.right = deleteNode(root.right, temp.key); } }   // If the tree had only one node then return if (root == null) return root;   // STEP 2: UPDATE HEIGHT OF THE CURRENT NODE root.height = max(height(root.left), height(root.right)) + 1;   // STEP 3: GET THE BALANCE FACTOR // OF THIS NODE (to check whether // this node became unbalanced) int balance = getBalance(root);   // If this node becomes unbalanced, // then there are 4 cases // Left Left Case if (balance > 1 && getBalance(root.left) >= 0) return rightRotate(root);   // Left Right Case if (balance > 1 && getBalance(root.left) < 0) { root.left = leftRotate(root.left); return rightRotate(root); }   // Right Right Case if (balance < -1 && getBalance(root.right) <= 0) return leftRotate(root);   // Right Left Case if (balance < -1 && getBalance(root.right) > 0) { root.right = rightRotate(root.right); return leftRotate(root); }   return root; }   // A utility function to print preorder traversal of // the tree. The function also prints height of every // node void preOrder(Node node) { if (node != null) { Console.Write(node.key + " "); preOrder(node.left); preOrder(node.right); } }   // Driver code public static void Main() { AVLTree tree = new AVLTree();   /* Constructing tree given in the above figure */ tree.root = tree.insert(tree.root, 9); tree.root = tree.insert(tree.root, 5); tree.root = tree.insert(tree.root, 10); tree.root = tree.insert(tree.root, 0); tree.root = tree.insert(tree.root, 6); tree.root = tree.insert(tree.root, 11); tree.root = tree.insert(tree.root, -1); tree.root = tree.insert(tree.root, 1); tree.root = tree.insert(tree.root, 2);   /* The constructed AVL Tree would be 9 / \ 1 10 / \ \ 0 5 11 / / \ -1 2 6 */ Console.WriteLine("Preorder traversal of "+ "constructed tree is : "); tree.preOrder(tree.root);   tree.root = tree.deleteNode(tree.root, 10);   /* The AVL Tree after deletion of 10 1 / \ 0 9 /     / \ -1 5 11 / \ 2 6 */ Console.WriteLine(""); Console.WriteLine("Preorder traversal after "+ "deletion of 10 :"); tree.preOrder(tree.root); } }   /* This code contributed by PrinciRaj1992 */ | | — |

Javascript

| <script>   // JavaScript program for deletion in AVL Tree   class Node { constructor(d) { this.left = null; this.right = null; this.key = d; this.height = 1; } }   let root;   // A utility function to get height of the tree function height(N) { if (N == null) return 0; return N.height; }   // A utility function to get maximum of two integers function max(a, b) { return (a > b) ? a : b; }   // A utility function to right rotate subtree rooted with y // See the diagram given above. function rightRotate(y) { let x = y.left; let T2 = x.right;   // Perform rotation x.right = y; y.left = T2;   // Update heights y.height = max(height(y.left), height(y.right)) + 1; x.height = max(height(x.left), height(x.right)) + 1;   // Return new root return x; }   // A utility function to left rotate subtree rooted with x // See the diagram given above. function leftRotate(x) { let y = x.right; let T2 = y.left;   // Perform rotation y.left = x; x.right = T2;   // Update heights x.height = max(height(x.left), height(x.right)) + 1; y.height = max(height(y.left), height(y.right)) + 1;   // Return new root return y; }   // Get Balance factor of node N function getBalance(N) { if (N == null) return 0; return height(N.left) - height(N.right); }   function insert(node, key) { /* 1. Perform the normal BST rotation */ if (node == null) return (new Node(key));   if (key < node.key) node.left = insert(node.left, key); else if (key > node.key) node.right = insert(node.right, key); else // Equal keys not allowed return node;   /* 2. Update height of this ancestor node */ node.height = 1 + max(height(node.left), height(node.right));   /* 3. Get the balance factor of this ancestor node to check whether this node became Wunbalanced */ let balance = getBalance(node);   // If this node becomes unbalanced, then // there are 4 cases Left Left Case if (balance > 1 && key < node.left.key) return rightRotate(node);   // Right Right Case if (balance < -1 && key > node.right.key) return leftRotate(node);   // Left Right Case if (balance > 1 && key > node.left.key) { node.left = leftRotate(node.left); return rightRotate(node); }   // Right Left Case if (balance < -1 && key < node.right.key) { node.right = rightRotate(node.right); return leftRotate(node); }   /* return the (unchanged) node pointer */ return node; }   /* Given a non-empty binary search tree, return the node with minimum key value found in that tree. Note that the entire tree does not need to be searched. */ function minValueNode(node) { let current = node;   /* loop down to find the leftmost leaf */ while (current.left != null) current = current.left;   return current; }   function deleteNode(root, key) { // STEP 1: PERFORM STANDARD BST DELETE if (root == null) return root;   // If the key to be deleted is smaller than // the root's key, then it lies in left subtree if (key < root.key) root.left = deleteNode(root.left, key);   // If the key to be deleted is greater than the // root's key, then it lies in right subtree else if (key > root.key) root.right = deleteNode(root.right, key);   // if key is same as root's key, then this is the node // to be deleted else {   // node with only one child or no child if ((root.left == null) || (root.right == null)) { let temp = null; if (temp == root.left) temp = root.right; else temp = root.left;   // No child case if (temp == null) { temp = root; root = null; } else // One child case root = temp; // Copy the contents of // the non-empty child } else {   // node with two children: Get the inorder // successor (smallest in the right subtree) let temp = minValueNode(root.right);   // Copy the inorder successor's data to this node root.key = temp.key;   // Delete the inorder successor root.right = deleteNode(root.right, temp.key); } }   // If the tree had only one node then return if (root == null) return root;   // STEP 2: UPDATE HEIGHT OF THE CURRENT NODE root.height = max(height(root.left), height(root.right)) + 1;   // STEP 3: GET THE BALANCE FACTOR OF THIS NODE (to check whether // this node became unbalanced) let balance = getBalance(root);   // If this node becomes unbalanced, then there are 4 cases // Left Left Case if (balance > 1 && getBalance(root.left) >= 0) return rightRotate(root);   // Left Right Case if (balance > 1 && getBalance(root.left) < 0) { root.left = leftRotate(root.left); return rightRotate(root); }   // Right Right Case if (balance < -1 && getBalance(root.right) <= 0) return leftRotate(root);   // Right Left Case if (balance < -1 && getBalance(root.right) > 0) { root.right = rightRotate(root.right); return leftRotate(root); }   return root; }   // A utility function to print preorder traversal of // the tree. The function also prints height of every // node function preOrder(node) { if (node != null) { document.write(node.key + " "); preOrder(node.left); preOrder(node.right); } }   /* Constructing tree given in the above figure */ root = insert(root, 9); root = insert(root, 5); root = insert(root, 10); root = insert(root, 0); root = insert(root, 6); root = insert(root, 11); root = insert(root, -1); root = insert(root, 1); root = insert(root, 2);   /* The constructed AVL Tree would be 9 / \ 1 10 / \ \ 0 5 11 / / \ -1 2 6 */ document.write( "Preorder traversal of the constructed AVL tree is : " + "</br>"); preOrder(root);   root = deleteNode(root, 10);   /* The AVL Tree after deletion of 10 1 / \ 0 9 /     / \ -1 5 11 / \ 2 6 */ document.write("</br>"); document.write("Preorder traversal after "+ "deletion of 10 :" + "</br>"); preOrder(root);   </script> | | — |

Output:  

Preorder traversal of the constructed AVL tree is 
9 1 0 -1 5 2 6 10 11 
Preorder traversal after deletion of 10 
1 0 -1 9 5 2 6 11 

Time Complexity: The rotation operations (left and right rotate) take constant time as only few pointers are being changed there. Updating the height and getting the balance factor also take constant time. So the time complexity of AVL delete remains same as BST delete which is O(h) where h is height of the tree. Since AVL tree is balanced, the height is O(Logn). So time complexity of AVL delete is O(Log n). 
Auxiliary Space: O(1), since no extra space is used.

Advantages Of AVL Trees

• It is always height balanced
• Height Never Goes Beyond LogN, where N is the number of nodes
• It give better search than compared to binary search tree
• It has self balancing capabilities

Summary of AVL Trees

• These are self-balancing binary search trees.
• Balancing Factor ranges -1, 0, and +1.
• When balancing factor goes beyond the range require rotations to be performed
• Insert, delete, and search time is O(log N).
• AVL tree are mostly used where search is more frequent compared to insert and delete operation.

Previous

Insertion, Searching and Deletion in AVL trees containing a parent node pointer

Next

How is an AVL tree different from a B-tree?

---

Introduction of B-Tree ======================

The limitations of traditional binary search trees can be frustrating. Meet the B-Tree, the multi-talented data structure that can handle massive amounts of data with ease. When it comes to storing and searching large amounts of data, traditional binary search trees can become impractical due to their poor performance and high memory usage. B-Trees, also known as B-Tree or Balanced Tree, are a type of self-balancing tree that was specifically designed to overcome these limitations.

Unlike traditional binary search trees, B-Trees are characterized by the large number of keys that they can store in a single node, which is why they are also known as “large key” trees. Each node in a B-Tree can contain multiple keys, which allows the tree to have a larger branching factor and thus a shallower height. This shallow height leads to less disk I/O, which results in faster search and insertion operations. B-Trees are particularly well suited for storage systems that have slow, bulky data access such as hard drives, flash memory, and CD-ROMs.

B-Trees maintains balance by ensuring that each node has a minimum number of keys, so the tree is always balanced. This balance guarantees that the time complexity for operations such as insertion, deletion, and searching is always O(log n), regardless of the initial shape of the tree.

**Time Complexity of B-Tree:**

Sr. No.	Algorithm	Time Complexity
1.	Search	O(log n)
2.	Insert	O(log n)
3.	Delete	O(log n)

**Note:** “n” is the total number of elements in the B-tree

**Properties of B-Tree:**

• All leaves are at the same level.
• B-Tree is defined by the term minimum degree ‘**t‘. The value of ‘t**‘ depends upon disk block size.
• Every node except the root must contain at least t-1 keys. The root may contain a minimum of **1** key.
• All nodes (including root) may contain at most (**2*t – 1**) keys.
• Number of children of a node is equal to the number of keys in it plus **1**.
• All keys of a node are sorted in increasing order. The child between two keys **k1** and **k2** contains all keys in the range from **k1** and **k2**.
• B-Tree grows and shrinks from the root which is unlike Binary Search Tree. Binary Search Trees grow downward and also shrink from downward.
• Like other balanced Binary Search Trees, the time complexity to search, insert, and delete is O(log n).
• Insertion of a Node in B-Tree happens only at Leaf Node.

Following is an example of a B-Tree of minimum order 5 
**Note:** that in practical B-Trees, the value of the minimum order is much more than 5. 
 

We can see in the above diagram that all the leaf nodes are at the same level and all non-leafs have no empty sub-tree and have keys one less than the number of their children.

**Interesting Facts about B-Trees:**

• The minimum height of the B-Tree that can exist with n number of nodes and m is the maximum number of children of a node can have is:  
• The maximum height of the B-Tree that can exist with n number of nodes and t is the minimum number of children that a non-root node can have is:   and  

**Traversal in B-Tree:**

Traversal is also similar to Inorder traversal of Binary Tree. We start from the leftmost child, recursively print the leftmost child, then repeat the same process for the remaining children and keys. In the end, recursively print the rightmost child. 

**Search Operation in B-Tree:**

Search is similar to the search in Binary Search Tree. Let the key to be searched is k. 

• Start from the root and recursively traverse down.
• For every visited non-leaf node, 
  • If the node has the key, we simply return the node.
  • Otherwise, we recur down to the appropriate child (The child which is just before the first greater key) of the node.
• If we reach a leaf node and don’t find k in the leaf node, then return NULL.

Searching a B-Tree is similar to searching a binary tree. The algorithm is similar and goes with recursion. At each level, the search is optimized as if the key value is not present in the range of the parent then the key is present in another branch. As these values limit the search they are also known as limiting values or separation values. If we reach a leaf node and don’t find the desired key then it will display NULL.

**Algorithm for Searching an Element in a B-Tree:-**

C++

| struct Node {int n;int key[MAX_KEYS];Node* child[MAX_CHILDREN];bool leaf;}; Node* BtreeSearch(Node* x, int k) {int i = 0;while (i < x->n && k > x->key[i]) {i++;}if (i < x->n && k == x->key[i]) {return x;}if (x->leaf) {return nullptr;}return BtreeSearch(x->child[i], k);} | | — |

C

| BtreeSearch(x, k)i = 1 // n[x] means number of keys in x nodewhile i ? n[x] and k ? keyi[x]do i = i + 1if i  n[x] and k = keyi[x]then return (x, i) if leaf [x]then return NILelsereturn BtreeSearch(ci[x], k) | | — |

Java

| class Node {int n;int[] key = new int[MAX_KEYS];Node[] child = new Node[MAX_CHILDREN];boolean leaf;} Node BtreeSearch(Node x, int k) {int i = 0;while (i < x.n && k >= x.key[i]) {i++;}if (i < x.n && k == x.key[i]) {return x;}if (x.leaf) {return null;}return BtreeSearch(x.child[i], k);} | | — |

Python3

| class Node:def __init__(self):self.n = 0self.key = [0] * MAX_KEYSself.child = [None] * MAX_CHILDRENself.leaf = True def BtreeSearch(x, k):i = 0while i < x.n and k >= x.key[i]:i += 1if i < x.n and k == x.key[i]:return xif x.leaf:return Nonereturn BtreeSearch(x.child[i], k) | | — |

C#

| class Node {public int n;public int[] key = new int[MAX_KEYS];public Node[] child = new Node[MAX_CHILDREN];public bool leaf;} Node BtreeSearch(Node x, int k) {int i = 0;while (i < x.n && k >= x.key[i]) {i++;}if (i < x.n && k == x.key[i]) {return x;}if (x.leaf) {return null;}return BtreeSearch(x.child[i], k);} | | — |

Javascript

| // Define a Node class with properties n, key, child, and leafclass Node {constructor() {this.n = 0;this.key = new Array(MAX_KEYS);this.child = new Array(MAX_CHILDREN);this.leaf = false;}} // Define a function BtreeSearch that takes in a Node object x and an integer kfunction BtreeSearch(x, k) {let i = 0;while (i < x.n && k >= x.key[i]) {i++;}if (i < x.n && k == x.key[i]) {return x;}if (x.leaf) {return null;}return BtreeSearch(x.child[i], k);} | | — |

**Examples:**

**Input:** Search 120 in the given B-Tree. 
 

 
**Solution:** 
 

 

 

In this example, we can see that our search was reduced by just limiting the chances where the key containing the value could be present. Similarly if within the above example we’ve to look for 180, then the control will stop at step 2 because the program will find that the key 180 is present within the current node. And similarly, if it’s to seek out 90 then as 90 < 100 so it’ll go to the left subtree automatically, and therefore the control flow will go similarly as shown within the above example.

Below is the implementation of the above approach:

C++

| // C++ implementation of search() and traverse() methods#include <iostream>using namespace std; // A BTree nodeclass BTreeNode {int* keys; // An array of keysint t; // Minimum degree (defines the range for number// of keys)BTreeNode** C; // An array of child pointersint n; // Current number of keysbool leaf; // Is true when node is leaf. Otherwise falsepublic:BTreeNode(int _t, bool _leaf); // Constructor // A function to traverse all nodes in a subtree rooted// with this nodevoid traverse(); // A function to search a key in the subtree rooted with// this node.BTreeNode*search(int k); // returns NULL if k is not present. // Make the BTree friend of this so that we can access// private members of this class in BTree functionsfriend class BTree;}; // A BTreeclass BTree {BTreeNode* root; // Pointer to root nodeint t; // Minimum degreepublic:// Constructor (Initializes tree as empty)BTree(int _t){root = NULL;t = _t;} // function to traverse the treevoid traverse(){if (root != NULL)root->traverse();} // function to search a key in this treeBTreeNode* search(int k){return (root == NULL) ? NULL : root->search(k);}}; // Constructor for BTreeNode classBTreeNode::BTreeNode(int _t, bool _leaf){// Copy the given minimum degree and leaf propertyt = _t;leaf = _leaf; // Allocate memory for maximum number of possible keys// and child pointerskeys = new int[2 * t - 1];C = new BTreeNode*[2 * t]; // Initialize the number of keys as 0n = 0;} // Function to traverse all nodes in a subtree rooted with// this nodevoid BTreeNode::traverse(){// There are n keys and n+1 children, traverse through n// keys and first n childrenint i;for (i = 0; i < n; i++) {// If this is not leaf, then before printing key[i],// traverse the subtree rooted with child C[i].if (leaf == false)C[i]->traverse();cout << " " << keys[i];} // Print the subtree rooted with last childif (leaf == false)C[i]->traverse();} // Function to search key k in subtree rooted with this nodeBTreeNode* BTreeNode::search(int k){// Find the first key greater than or equal to kint i = 0;while (i < n && k > keys[i])i++; // If the found key is equal to k, return this nodeif (keys[i] == k)return this; // If the key is not found here and this is a leaf nodeif (leaf == true)return NULL; // Go to the appropriate childreturn C[i]->search(k);} | | — |

Java

| // Java program to illustrate the sum of two numbers // A BTreeclass Btree {public BTreeNode root; // Pointer to root nodepublic int t; // Minimum degree // Constructor (Initializes tree as empty)Btree(int t){this.root = null;this.t = t;} // function to traverse the treepublic void traverse(){if (this.root != null)this.root.traverse();System.out.println();} // function to search a key in this treepublic BTreeNode search(int k){if (this.root == null)return null;elsereturn this.root.search(k);}} // A BTree nodeclass BTreeNode {int[] keys; // An array of keysint t; // Minimum degree (defines the range for number// of keys)BTreeNode[] C; // An array of child pointersint n; // Current number of keysbooleanleaf; // Is true when node is leaf. Otherwise false // ConstructorBTreeNode(int t, boolean leaf){this.t = t;this.leaf = leaf;this.keys = new int[2 * t - 1];this.C = new BTreeNode[2 * t];this.n = 0;} // A function to traverse all nodes in a subtree rooted// with this nodepublic void traverse(){ // There are n keys and n+1 children, traverse// through n keys and first n childrenint i = 0;for (i = 0; i < this.n; i++) { // If this is not leaf, then before printing// key[i], traverse the subtree rooted with// child C[i].if (this.leaf == false) {C[i].traverse();}System.out.print(keys[i] + " ");} // Print the subtree rooted with last childif (leaf == false)C[i].traverse();} // A function to search a key in the subtree rooted with// this node.BTreeNode search(int k){ // returns NULL if k is not present. // Find the first key greater than or equal to kint i = 0;while (i < n && k > keys[i])i++; // If the found key is equal to k, return this nodeif (keys[i] == k)return this; // If the key is not found here and this is a leaf// nodeif (leaf == true)return null; // Go to the appropriate childreturn C[i].search(k);}} | | — |

Python3

| # Create a nodeclass BTreeNode:def __init__(self, leaf=False):self.leaf = leafself.keys = []self.child = []  # Treeclass BTree:def __init__(self, t):self.root = BTreeNode(True)self.t = t # Insert nodedef insert(self, k):root = self.rootif len(root.keys) == (2 * self.t) - 1:temp = BTreeNode()self.root = temptemp.child.insert(0, root)self.split_child(temp, 0)self.insert_non_full(temp, k)else:self.insert_non_full(root, k) # Insert nonfulldef insert_non_full(self, x, k):i = len(x.keys) - 1if x.leaf:x.keys.append((None, None))while i >= 0 and k[0] < x.keys[i][0]:x.keys[i + 1] = x.keys[i]i -= 1x.keys[i + 1] = kelse:while i >= 0 and k[0] < x.keys[i][0]:i -= 1i += 1if len(x.child[i].keys) == (2 * self.t) - 1:self.split_child(x, i)if k[0] > x.keys[i][0]:i += 1self.insert_non_full(x.child[i], k) # Split the childdef split_child(self, x, i):t = self.ty = x.child[i]z = BTreeNode(y.leaf)x.child.insert(i + 1, z)x.keys.insert(i, y.keys[t - 1])z.keys = y.keys[t: (2 * t) - 1]y.keys = y.keys[0: t - 1]if not y.leaf:z.child = y.child[t: 2 * t]y.child = y.child[0: t - 1] # Print the treedef print_tree(self, x, l=0):print("Level ", l, " ", len(x.keys), end=":")for i in x.keys:print(i, end=" ")print()l += 1if len(x.child) > 0:for i in x.child:self.print_tree(i, l) # Search key in the treedef search_key(self, k, x=None):if x is not None:i = 0while i < len(x.keys) and k > x.keys[i][0]:i += 1if i < len(x.keys) and k == x.keys[i][0]:return (x, i)elif x.leaf:return Noneelse:return self.search_key(k, x.child[i]) else:return self.search_key(k, self.root)  def main():B = BTree(3) for i in range(10):B.insert((i, 2 * i)) B.print_tree(B.root) if B.search_key(8) is not None:print("\nFound")else:print("\nNot Found")  if __name__ == '__main__':main() | | — |

C#

| // C# program to illustrate the sum of two numbersusing System; // A BTreeclass Btree {public BTreeNode root; // Pointer to root nodepublic int t; // Minimum degree // Constructor (Initializes tree as empty)Btree(int t){this.root = null;this.t = t;} // function to traverse the treepublic void traverse(){if (this.root != null)this.root.traverse();Console.WriteLine();} // function to search a key in this treepublic BTreeNode search(int k){if (this.root == null)return null;elsereturn this.root.search(k);}} // A BTree nodeclass BTreeNode {int[] keys; // An array of keysint t; // Minimum degree (defines the range for number// of keys)BTreeNode[] C; // An array of child pointersint n; // Current number of keysbool leaf; // Is true when node is leaf. Otherwise false // ConstructorBTreeNode(int t, bool leaf){this.t = t;this.leaf = leaf;this.keys = new int[2 * t - 1];this.C = new BTreeNode[2 * t];this.n = 0;} // A function to traverse all nodes in a subtree rooted// with this nodepublic void traverse(){ // There are n keys and n+1 children, traverse// through n keys and first n childrenint i = 0;for (i = 0; i < this.n; i++) { // If this is not leaf, then before printing// key[i], traverse the subtree rooted with// child C[i].if (this.leaf == false) {C[i].traverse();}Console.Write(keys[i] + " ");} // Print the subtree rooted with last childif (leaf == false)C[i].traverse();} // A function to search a key in the subtree rooted with// this node.public BTreeNode search(int k){ // returns NULL if k is not present. // Find the first key greater than or equal to kint i = 0;while (i < n && k > keys[i])i++; // If the found key is equal to k, return this nodeif (keys[i] == k)return this; // If the key is not found here and this is a leaf// nodeif (leaf == true)return null; // Go to the appropriate childreturn C[i].search(k);}} // This code is contributed by Rajput-Ji | | — |

Javascript

| // Javascript program to illustrate the sum of two numbers // A BTreeclass Btree{ // Constructor (Initializes tree as empty)constructor(t){this.root = null;this.t = t;} // function to traverse the treetraverse(){if (this.root != null)this.root.traverse();document.write("<br>");} // function to search a key in this treesearch(k){if (this.root == null)return null;elsereturn this.root.search(k);} } // A BTree nodeclass BTreeNode{// Constructorconstructor(t,leaf){this.t = t;this.leaf = leaf;this.keys = new Array(2 * t - 1);this.C = new Array(2 * t);this.n = 0;}// A function to traverse all nodes in a subtree rooted with this nodetraverse(){// There are n keys and n+1 children, traverse through n keys// and first n childrenlet i = 0;for (i = 0; i < this.n; i++) { // If this is not leaf, then before printing key[i],// traverse the subtree rooted with child C[i].if (this.leaf == false) {C[i].traverse();}document.write(keys[i] + " ");} // Print the subtree rooted with last childif (leaf == false)C[i].traverse();} // A function to search a key in the subtree rooted with this node.search(k) // returns NULL if k is not present.{ // Find the first key greater than or equal to klet i = 0;while (i < n && k > keys[i])i++; // If the found key is equal to k, return this nodeif (keys[i] == k)return this; // If the key is not found here and this is a leaf nodeif (leaf == true)return null; // Go to the appropriate childreturn C[i].search(k);}} // This code is contributed by patel2127 | | — |

**Note:** The above code doesn’t contain the driver program. We will be covering the complete program in our next post on B-Tree Insertion.

There are two conventions to define a B-Tree, one is to define by minimum degree, second is to define by order. We have followed the minimum degree convention and will be following the same in coming posts on B-Tree. The variable names used in the above program are also kept the same

**Applications of B-Trees:**

• It is used in large databases to access data stored on the disk
• Searching for data in a data set can be achieved in significantly less time using the B-Tree
• With the indexing feature, multilevel indexing can be achieved.
• Most of the servers also use the B-tree approach.
• B-Trees are used in CAD systems to organize and search geometric data.
• B-Trees are also used in other areas such as natural language processing, computer networks, and cryptography.

**Advantages of B-Trees:**

• B-Trees have a guaranteed time complexity of O(log n) for basic operations like insertion, deletion, and searching, which makes them suitable for large data sets and real-time applications.
• B-Trees are self-balancing.
• High-concurrency and high-throughput.
• Efficient storage utilization.

**Disadvantages of B-Trees:**

• B-Trees are based on disk-based data structures and can have a high disk usage.
• Not the best for all cases.
• Slow in comparison to other data structures.

Insertion and Deletion:
B-Tree Insertion 
B-Tree Deletion

Next

Insert Operation in B-Tree

---