Introduction to Queue – Data Structure and Algorithm Tutorials
**Queue** is a linear data structure that follows **FIFO (First In First Out) Principle**, so the first element inserted is the first to be popped out. In this article, we will cover all the basics of Queue, Operations on Queue, its implementation, advantages, disadvantages which will help you solve all the problems based on Queue.

Table of Content
- What is Queue?
- Representation of Queue Data Structure
- Types of Queue
- Basic Operations in Queue
- Enqueue Operation in Queue
- Dequeue Operation in Queue
- Front Operation in Queue
- Rear Operation in Queue
- isEmpty Operation in Queue
- Queue Implementation
- Complexity Analysis of Operations on Queue
- Applications of Queue
- Advantages of Queue
- Disadvantages of Queue
- FAQs (Frequently asked questions) on Queue **What is Queue?** ———————-
**Queue** is a linear data structure that is open at both ends and the operations are performed in First In First Out (FIFO) order.
We define a queue to be a list in which all additions to the list are made at one end (**back of the queue), and all deletions from the list are made at the other end(front of the queue**). The element which is first pushed into the order, the delete operation is first performed on that.
**FIFO Principle of Queue:**
- A Queue is like a line waiting to purchase tickets, where the first person in line is the first person served. (i.e. First Come First Serve).
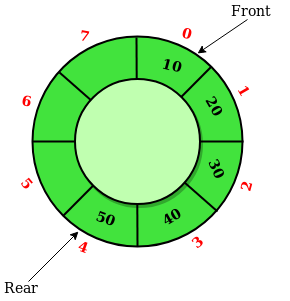
- Position of the entry in a queue ready to be served, that is, the first entry that will be removed from the queue, is called the **front** of the queue(sometimes, **head** of the queue). Similarly, the position of the last entry in the queue, that is, the one most recently added, is called the **rear** (or the **tail**) of the queue.
.webp) **Representation of Queue Data Structure:**
**Representation of Queue Data Structure:**
The image below shows how we represent Queue Data Structure:
 Types of Queue:
————————————————————————————————
Types of Queue:
————————————————————————————————
Queue data structure can be classified into 4 types:
.webp)
There are different types of queues:
- **Simple Queue:** Simple Queue simply follows **FIFO** Structure. We can only insert the element at the back and remove the element from the front of the queue.
- [**Double-Ended Queue (Dequeue)](https://www.geeksforgeeks.org/deque-set-1-introduction-applications/):** In a double-ended queue the insertion and deletion operations, both can be performed from both ends. They are of two types:
- **Input Restricted Queue:** This is a simple queue. In this type of queue, the input can be taken from only one end but deletion can be done from any of the ends.
- **Output Restricted Queue:** This is also a simple queue. In this type of queue, the input can be taken from both ends but deletion can be done from only one end.
- **Circular Queue:** This is a special type of queue where the last position is connected back to the first position. Here also the operations are performed in FIFO order.
- [**Priority Queue](https://www.geeksforgeeks.org/priority-queue-set-1-introduction/):** A priority queue is a special queue where the elements are accessed based on the priority assigned to them. They are of two types:
- **Ascending Priority Queue:** In Ascending Priority Queue, the elements are arranged in increasing order of their priority values. Element with smallest priority value is popped first.
- **Descending Priority Queue:** In Descending Priority Queue, the elements are arranged in decreasing order of their priority values. Element with largest priority is popper first.
Basic Operations in Queue:
Some of the basic operations for Queue in Data Structure are:
- **Enqueue:** Adds (or stores) an element to the end of the queue..
- **Dequeue:** Removal of elements from the queue.
- **Peek or front:** Acquires the data element available at the front node of the queue without deleting it.
- **rear:** This operation returns the element at the rear end without removing it.
- **isFull**: Validates if the queue is full.
- **isEmpty**: Checks if the queue is empty.
There are a few supporting operations (auxiliary operations):
**1. Enqueue Operation in Queue:**
Enqueue() operation in Queue **adds (or stores) an element to the end of the queue**.
The following steps should be taken to enqueue (insert) data into a queue:
- **Step 1:** Check if the queue is full.
- **Step 2:** If the queue is full, return overflow error and exit.
- **Step 3:** If the queue is not full, increment the rear pointer to point to the next empty space.
- **Step 4:** Add the data element to the queue location, where the rear is pointing.
- **Step 5:** return success.
Implementation of Enqueue:
void queueEnqueue(int data)
{
// Check queue is full or not
if (capacity == rear) {
printf("\nQueue is full\n");
return;
}
// Insert element at the rear
else {
queue[rear] = data;
rear++;
}
return;
}
void queueEnqueue(int data)
{
// Check queue is full or not
if (capacity == rear) {
System.out.println("\nQueue is full\n");
return;
}
// Insert element at the rear
else {
queue[rear] = data;
rear++;
}
return;
}
// This code is contributed by aadityapburujwale
**2. Dequeue Operation in Queue:**
Removes (or access) the first element from the queue.
The following steps are taken to perform the dequeue operation:
- **Step 1:** Check if the queue is empty.
- **Step 2:** If the queue is empty, return the underflow error and exit.
- **Step 3:** If the queue is not empty, access the data where the front is pointing.
- **Step 4:** Increment the front pointer to point to the next available data element.
- **Step 5:** The Return success.
Implementation of dequeue:
void queueDequeue()
{
// If queue is empty
if (front == rear) {
printf("\nQueue is empty\n");
return;
}
// Shift all the elements from index 2
// till rear to the left by one
else {
for (int i = 0; i < rear - 1; i++) {
queue[i] = queue[i + 1];
}
// decrement rear
rear--;
}
return;
}
void queueDequeue()
{
// If queue is empty
if (front == rear) {
System.out.println("\nQueue is empty\n");
return;
}
// Shift all the elements from index 2
// till rear to the left by one
else {
for (int i = 0; i < rear - 1; i++) {
queue[i] = queue[i + 1];
}
// decrement rear
rear--;
}
return;
}
// This code is contributed by aadityapburujwale
**3. Front Operation in Queue:**
This operation returns the element at the front end without removing it.
// Function to get front of queue
int front(Queue* queue)
{
if (isempty(queue))
return INT_MIN;
return queue->arr[queue->front];
}
// Function to get front of queue
int front(Queue queue)
{
if (isempty(queue))
return Integer.MIN_VALUE;
return queue.arr[queue.front];
}
// This code is contributed by aadityapburujwale
**4. Rear Operation in Queue:**
This operation returns the element at the rear end without removing it.
int rear(queue<int>& myQueue)
{
queue<int> tempQueue = myQueue;
while (tempQueue.size() > 1) {
tempQueue.pop();
}
return tempQueue.front();
}
public static int rear(Queue<Integer> myQueue)
{
if (myQueue.isEmpty()) {
System.out.println("Queue is empty.");
return -1;
}
int rearElement = -1;
while (!myQueue.isEmpty()) {
rearElement = myQueue.poll();
}
return rearElement;
}
**5. isEmpty Operation in Queue:**
This operation returns a boolean value that indicates whether the queue is empty or not.
// This function will check whether
// the queue is empty or not:
bool isEmpty()
{
if (front == -1)
return true;
else
return false;
}
// This function will check whether
// the queue is empty or not:
boolean isEmpty()
{
if (front == -1)
return true;
else
return false;
}
// This code is contributed by aadityapburujwale
**6. isFull Operation in Queue:**
This operation returns a boolean value that indicates whether the queue is full or not.
// This function will check
// whether the queue is full or not.
bool isFull()
{
if (front == 0 && rear == MAX_SIZE - 1) {
return true;
}
return false;
}
// This function will check
// whether the queue is full or not.
boolean isFull()
{
if (front == 0 && rear == MAX_SIZE - 1) {
return true;
}
return false;
}
// This code is contributed by aadityapburujwale
Queue Implementation:
Queue can be implemented using following data structures:
We have discussed the implementation of Queue below:
// Implementation of queue(enqueue, dequeue).
#include <bits/stdc++.h>
using namespace std;
class Queue {
public:
int front, rear, size;
unsigned cap;
int* arr;
};
Queue* createQueue(unsigned cap)
{
Queue* queue = new Queue();
queue->cap = cap;
queue->front = queue->size = 0;
queue->rear = cap - 1;
queue->arr = new int[(queue->cap * sizeof(int))];
return queue;
}
int isFull(Queue* queue)
{
return (queue->size == queue->cap);
}
int isempty(Queue* queue) { return (queue->size == 0); }
// Function to add an item to the queue.
// It changes rear and size.
void enqueue(Queue* queue, int item)
{
if (isFull(queue))
return;
queue->rear = (queue->rear + 1) % queue->cap;
queue->arr[queue->rear] = item;
queue->size = queue->size + 1;
cout << item << " enqueued to queue\n";
}
// Function to remove an item from queue.
// It changes front and size
int dequeue(Queue* queue)
{
if (isempty(queue))
return INT_MIN;
int item = queue->arr[queue->front];
queue->front = (queue->front + 1) % queue->cap;
queue->size = queue->size - 1;
return item;
}
int front(Queue* queue)
{
if (isempty(queue))
return INT_MIN;
return queue->arr[queue->front];
}
int rear(Queue* queue)
{
if (isempty(queue))
return INT_MIN;
return queue->arr[queue->rear];
}
// Driver code
int main()
{
Queue* queue = createQueue(1000);
enqueue(queue, 10);
enqueue(queue, 20);
enqueue(queue, 30);
enqueue(queue, 40);
cout << dequeue(queue);
cout << " dequeued from queue\n";
cout << "Front item is " << front(queue) << endl;
cout << "Rear item is " << rear(queue);
return 0;
}
// Java program for array
// implementation of queue
// A class to represent a queue
class Queue {
int front, rear, size;
int capacity;
int array[];
public Queue(int capacity)
{
this.capacity = capacity;
front = this.size = 0;
rear = capacity - 1;
array = new int[this.capacity];
}
// Queue is full when size becomes
// equal to the capacity
boolean isFull(Queue queue)
{
return (queue.size == queue.capacity);
}
// Queue is empty when size is 0
boolean isEmpty(Queue queue)
{
return (queue.size == 0);
}
// Method to add an item to the queue.
// It changes rear and size
void enqueue(int item)
{
if (isFull(this))
return;
this.rear = (this.rear + 1) % this.capacity;
this.array[this.rear] = item;
this.size = this.size + 1;
System.out.println(item + " enqueued to queue");
}
// Method to remove an item from queue.
// It changes front and size
int dequeue()
{
if (isEmpty(this))
return Integer.MIN_VALUE;
int item = this.array[this.front];
this.front = (this.front + 1) % this.capacity;
this.size = this.size - 1;
return item;
}
// Method to get front of queue
int front()
{
if (isEmpty(this))
return Integer.MIN_VALUE;
return this.array[this.front];
}
// Method to get rear of queue
int rear()
{
if (isEmpty(this))
return Integer.MIN_VALUE;
return this.array[this.rear];
}
}
// Driver class
public class Test {
public static void main(String[] args)
{
Queue queue = new Queue(1000);
queue.enqueue(10);
queue.enqueue(20);
queue.enqueue(30);
queue.enqueue(40);
System.out.println(queue.dequeue()
+ " dequeued from queue");
System.out.println("Front item is "
+ queue.front());
System.out.println("Rear item is " + queue.rear());
}
}
// This code is contributed by Susobhan Akhuli
Output
10 enqueued to queue
20 enqueued to queue
30 enqueued to queue
40 enqueued to queue
10 dequeued from queue
Front item is 20
Rear item is 40
Complexity Analysis of Operations on Queue ——————————————
| **Operations** | **Time Complexity** | **Space Complexity** |
|---|---|---|
| **Enqueue** | O(1) | O(1) |
| **Dequeue** | O(1) | O(1) |
| Front | O(1) | O(1) |
| Back | O(1) | O(1) |
| isEmpty | O(1) | O(1) |
| isFull | O(1) | O(1) |
**Applications of Queue:**
Application of queue is common. In a computer system, there may be queues of tasks waiting for the printer, for access to disk storage, or even in a time-sharing system, for use of the CPU. Within a single program, there may be multiple requests to be kept in a queue, or one task may create other tasks, which must be done in turn by keeping them in a queue.
- Queue can be used in job scheduling like Printer Spooling.
- Queue can be used where we have a single resource and multiple consumers.
- In a network, a queue is used in devices such as a router/switch and mail queue.
- Queue can be used in various algorithm techniques like Breadth First Search, Topological Sort, etc.
Advantages of Queue:
- A large amount of data can be managed efficiently with ease.
- Operations such as insertion and deletion can be performed with ease as it follows the first in first out rule.
- Queues are useful when a particular service is used by multiple consumers.
- Queues are fast in speed for data inter-process communication.
- Queues can be used in the implementation of other data structures.
Disadvantages of Queue:
- The operations such as insertion and deletion of elements from the middle are time consuming.
- Searching an element takes O(N) time.
- Maximum size of a queue must be defined prior in case of array implementation.
FAQs (Frequently asked questions) on Queue:
1. What data structure can be used to implement a priority queue?
Priority queues can be implemented using a variety of data structures, including linked lists, arrays, binary search trees, and heaps. Priority queues are best implemented using the heap data structure.
3. In data structures, what is a double-ended queue?
In a double-ended queue, elements can be inserted and removed at both ends.
4. What is better, a stack or a queue?
If you want things to come out in the order you put them in, use a queue. Stacks are useful when you want to reorder things after putting them in.
5. Is Queue a LIFO or FIFO?
Queue follows FIFO (First-In-First-Out) principle, so the element which is inserted first will be deleted first.
6. What are the four types of Queue?
The four types of Queue are: Simple Queue, Double-ended queue, Circular Queue and Priority Queue.
7. What are some real-life applications of Queue?
Real-life applications of queue include: Cashier Line in Stores, CPU Scheduling, Disk Scheduling, Serving requests on a shared resource like Printer.
8. What are some limitations of Queue?
Some of the limitations of Queue are: deletion of some middle element is not possible until all the elements before it are not deleted. Also random access of any element takes linear time complexity.
9. What are the different ways to implement a Queue?
Queue data structure can be implemented by using Arrays or by using Linked List. The Array implementation requires the size of the Queue to be specified at the time of declaration.
10. What are some common operations in Queue?
Some common operations on Queue are: Insertion or Enqueue, Deletion or Dequeue, Front, Rear, isFull, isEmpty, etc.
**Related articles:**
- Queue Operations
- Applications, Advantages and Disadvantages of Queue
- Maximum of all subarrays of size k
- Generate Binary Numbers
- Queue using two Stacks
- Reverse First K elements of Queue
Introduction and Array Implementation of Queue
Introduction and Array Implementation of Queue ==============================================
Similar to Stack, Queueis a linear data structure that follows a particular order in which the operations are performed for storing data. The order is First In First Out (FIFO). One can imagine a queue as a line of people waiting to receive something in sequential order which starts from the beginning of the line. It is an ordered list in which insertions are done at one end which is known as the rear and deletions are done from the other end known as the front. A good example of a queue is any queue of consumers for a resource where the consumer that came first is served first.
The difference between stacks and queues is in removing. In a stack we remove the item the most recently added; in a queue, we remove the item the least recently added.
Recommended PracticeImplement Queue using arrayTry It!
 Queue Data structure
Queue Data structure
Basic Operations on Queue:
- enqueue(): Inserts an element at the end of the queue i.e. at the rear end.
- dequeue(): This operation removes and returns an element that is at the front end of the queue.
- front(): This operation returns the element at the front end without removing it.
- rear(): This operation returns the element at the rear end without removing it.
- isEmpty(): This operation indicates whether the queue is empty or not.
- isFull(): This operation indicates whether the queue is full or not.
- size(): This operation returns the size of the queue i.e. the total number of elements it contains.
Types of Queues:
- Simple Queue: Simple queue also known as a linear queue is the most basic version of a queue. Here, insertion of an element i.e. the Enqueue operation takes place at the rear end and removal of an element i.e. the Dequeue operation takes place at the front end. Here problem is that if we pop some item from front and then rear reach to the capacity of the queue and although there are empty spaces before front means the queue is not full but as per condition in isFull() function, it will show that the queue is full then. To solve this problem we use circular queue.
- Circular Queue:In a circular queue, the element of the queue act as a circular ring. The working of a circular queue is similar to the linear queue except for the fact that the last element is connected to the first element. Its advantage is that the memory is utilized in a better way. This is because if there is an empty space i.e. if no element is present at a certain position in the queue, then an element can be easily added at that position using modulo capacity(%n).
- Priority Queue: This queue is a special type of queue. Its specialty is that it arranges the elements in a queue based on some priority. The priority can be something where the element with the highest value has the priority so it creates a queue with decreasing order of values. The priority can also be such that the element with the lowest value gets the highest priority so in turn it creates a queue with increasing order of values. In pre-define priority queue, C++ gives priority to highest value whereas Java gives priority to lowest value.
- Dequeue: Dequeue is also known as Double Ended Queue. As the name suggests double ended, it means that an element can be inserted or removed from both ends of the queue, unlike the other queues in which it can be done only from one end. Because of this property, it may not obey the First In First Out property.

Applications of Queue:
Queue is used when things don’t have to be processed immediately, but have to be processed in First In First Out order like Breadth First Search. This property of Queue makes it also useful in following kind of scenarios.
- When a resource is shared among multiple consumers. Examples include CPU scheduling, Disk Scheduling.
- When data is transferred asynchronously (data not necessarily received at same rate as sent) between two processes. Examples include IO Buffers, pipes, file IO, etc.
- Queue can be used as an essential component in various other data structures.
Array implementation Of Queue:
For implementing queue, we need to keep track of two indices, front and rear. We enqueue an item at the rear and dequeue an item from the front. If we simply increment front and rear indices, then there may be problems, the front may reach the end of the array. The solution to this problem is to increase front and rear in circular manner.
Steps for enqueue:
- Check the queue is full or not
- If full, print overflow and exit
- If queue is not full, increment tail and add the element
Steps for dequeue:
- Check queue is empty or not
- if empty, print underflow and exit
- if not empty, print element at the head and increment head
Below is a program to implement above operation on queue
C++
| // CPP program for array // implementation of queue #include <bits/stdc++.h> using namespace std; // A structure to represent a queue class Queue { public: int front, rear, size; unsigned capacity; int* array; }; // function to create a queue // of given capacity. // It initializes size of queue as 0 Queue* createQueue(unsigned capacity) { Queue* queue = new Queue(); queue->capacity = capacity; queue->front = queue->size = 0; // This is important, see the enqueue queue->rear = capacity - 1; queue->array = new int[queue->capacity]; return queue; } // Queue is full when size // becomes equal to the capacity int isFull(Queue* queue) { return (queue->size == queue->capacity); } // Queue is empty when size is 0 int isEmpty(Queue* queue) { return (queue->size == 0); } // Function to add an item to the queue. // It changes rear and size void enqueue(Queue* queue, int item) { if (isFull(queue)) return; queue->rear = (queue->rear + 1) % queue->capacity; queue->array[queue->rear] = item; queue->size = queue->size + 1; cout << item << " enqueued to queue\n"; } // Function to remove an item from queue. // It changes front and size int dequeue(Queue* queue) { if (isEmpty(queue)) return INT_MIN; int item = queue->array[queue->front]; queue->front = (queue->front + 1) % queue->capacity; queue->size = queue->size - 1; return item; } // Function to get front of queue int front(Queue* queue) { if (isEmpty(queue)) return INT_MIN; return queue->array[queue->front]; } // Function to get rear of queue int rear(Queue* queue) { if (isEmpty(queue)) return INT_MIN; return queue->array[queue->rear]; } // Driver code int main() { Queue* queue = createQueue(1000); enqueue(queue, 10); enqueue(queue, 20); enqueue(queue, 30); enqueue(queue, 40); cout << dequeue(queue) << " dequeued from queue\n"; cout << "Front item is " << front(queue) << endl; cout << "Rear item is " << rear(queue) << endl; return 0; } // This code is contributed by rathbhupendra |
| — |
C
| // C program for array implementation of queue #include <limits.h> #include <stdio.h> #include <stdlib.h> // A structure to represent a queue struct Queue { int front, rear, size; unsigned capacity; int* array; }; // function to create a queue // of given capacity. // It initializes size of queue as 0 struct Queue* createQueue(unsigned capacity) { struct Queue* queue = (struct Queue*)malloc( sizeof(struct Queue)); queue->capacity = capacity; queue->front = queue->size = 0; // This is important, see the enqueue queue->rear = capacity - 1; queue->array = (int*)malloc( queue->capacity * sizeof(int)); return queue; } // Queue is full when size becomes // equal to the capacity int isFull(struct Queue* queue) { return (queue->size == queue->capacity); } // Queue is empty when size is 0 int isEmpty(struct Queue* queue) { return (queue->size == 0); } // Function to add an item to the queue. // It changes rear and size void enqueue(struct Queue* queue, int item) { if (isFull(queue)) return; queue->rear = (queue->rear + 1) % queue->capacity; queue->array[queue->rear] = item; queue->size = queue->size + 1; printf("%d enqueued to queue\n", item); } // Function to remove an item from queue. // It changes front and size int dequeue(struct Queue* queue) { if (isEmpty(queue)) return INT_MIN; int item = queue->array[queue->front]; queue->front = (queue->front + 1) % queue->capacity; queue->size = queue->size - 1; return item; } // Function to get front of queue int front(struct Queue* queue) { if (isEmpty(queue)) return INT_MIN; return queue->array[queue->front]; } // Function to get rear of queue int rear(struct Queue* queue) { if (isEmpty(queue)) return INT_MIN; return queue->array[queue->rear]; } // Driver program to test above functions./ int main() { struct Queue* queue = createQueue(1000); enqueue(queue, 10); enqueue(queue, 20); enqueue(queue, 30); enqueue(queue, 40); printf("%d dequeued from queue\n\n", dequeue(queue)); printf("Front item is %d\n", front(queue)); printf("Rear item is %d\n", rear(queue)); return 0; } |
| — |
Java
| // Java program for array // implementation of queue // A class to represent a queue class Queue { int front, rear, size; int capacity; int array[]; public Queue(int capacity) { this.capacity = capacity; front = this.size = 0; rear = capacity - 1; array = new int[this.capacity]; } // Queue is full when size becomes // equal to the capacity boolean isFull(Queue queue) { return (queue.size == queue.capacity); } // Queue is empty when size is 0 boolean isEmpty(Queue queue) { return (queue.size == 0); } // Method to add an item to the queue. // It changes rear and size void enqueue(int item) { if (isFull(this)) return; this.rear = (this.rear + 1) % this.capacity; this.array[this.rear] = item; this.size = this.size + 1; System.out.println(item + " enqueued to queue"); } // Method to remove an item from queue. // It changes front and size int dequeue() { if (isEmpty(this)) return Integer.MIN_VALUE; int item = this.array[this.front]; this.front = (this.front + 1) % this.capacity; this.size = this.size - 1; return item; } // Method to get front of queue int front() { if (isEmpty(this)) return Integer.MIN_VALUE; return this.array[this.front]; } // Method to get rear of queue int rear() { if (isEmpty(this)) return Integer.MIN_VALUE; return this.array[this.rear]; } } // Driver class public class Test { public static void main(String[] args) { Queue queue = new Queue(1000); queue.enqueue(10); queue.enqueue(20); queue.enqueue(30); queue.enqueue(40); System.out.println(queue.dequeue() + " dequeued from queue\n"); System.out.println("Front item is " + queue.front()); System.out.println("Rear item is " + queue.rear()); } } // This code is contributed by Gaurav Miglani |
| — |
Python3
| # Python3 program for array implementation of queue # Class Queue to represent a queue class Queue: # __init__ function def __init__(self, capacity): self.front = self.size = 0 self.rear = capacity -1 self.Q = [None]*capacity self.capacity = capacity # Queue is full when size becomes # equal to the capacity def isFull(self): return self.size == self.capacity # Queue is empty when size is 0 def isEmpty(self): return self.size == 0 # Function to add an item to the queue. # It changes rear and size def EnQueue(self, item): if self.isFull(): print("Full") return self.rear = (self.rear + 1) % (self.capacity) self.Q[self.rear] = item self.size = self.size + 1 print("% s enqueued to queue" % str(item)) # Function to remove an item from queue. # It changes front and size def DeQueue(self): if self.isEmpty(): print("Empty") return print("% s dequeued from queue" % str(self.Q[self.front])) self.front = (self.front + 1) % (self.capacity) self.size = self.size -1 # Function to get front of queue def que_front(self): if self.isEmpty(): print("Queue is empty") print("Front item is", self.Q[self.front]) # Function to get rear of queue def que_rear(self): if self.isEmpty(): print("Queue is empty") print("Rear item is", self.Q[self.rear]) # Driver Code if __name__ == '__main__': queue = Queue(30) queue.EnQueue(10) queue.EnQueue(20) queue.EnQueue(30) queue.EnQueue(40) queue.DeQueue() queue.que_front() queue.que_rear() |
| — |
C#
| // C# program for array implementation of queue using System; namespace GeeksForGeeks { // A class to represent a linearqueue class Queue { private int[] ele; private int front; private int rear; private int max; public Queue(int size) { ele = new int[size]; front = 0; rear = -1; max = size; } // Function to add an item to the queue. // It changes rear and size public void enqueue(int item) { if (rear == max - 1) { Console.WriteLine("Queue Overflow"); return; } else { ele[++rear] = item; } } // Function to remove an item from queue. // It changes front and size public int dequeue() { if (front == rear + 1) { Console.WriteLine("Queue is Empty"); return -1; } else { Console.WriteLine(ele[front] + " dequeued from queue"); int p = ele[front++]; Console.WriteLine(); Console.WriteLine("Front item is {0}", ele[front]); Console.WriteLine("Rear item is {0} ", ele[rear]); return p; } } // Function to print queue. public void printQueue() { if (front == rear + 1) { Console.WriteLine("Queue is Empty"); return; } else { for (int i = front; i <= rear; i++) { Console.WriteLine(ele[i] + " enqueued to queue"); } } } } // Driver code class Program { static void Main() { Queue Q = new Queue(5); Q.enqueue(10); Q.enqueue(20); Q.enqueue(30); Q.enqueue(40); Q.printQueue(); Q.dequeue(); } } } |
| — |
Javascript
| <script> // Queue class class Queue { // Array is used to implement a Queue constructor() { this.items = []; } isEmpty() { // return true if the queue is empty. return this.items.length == 0; } enqueue(element) { // adding element to the queue this.items.push(element); document.write(element + " enqueued to queue<br>"); } dequeue() { // removing element from the queue // returns underflow when called // on empty queue if(this.isEmpty()) return "Underflow<br>"; return this.items.shift(); } front() { // returns the Front element of // the queue without removing it. if(this.isEmpty()) return "No elements in Queue<br>"; return this.items[0]; } rear() { // returns the Rear element of // the queue without removing it. if(this.isEmpty()) return "No elements in Queue<br>"; return this.items[this.items.length-1]; } } // creating object for queue class var queue = new Queue(); // Adding elements to the queue queue.enqueue(10); queue.enqueue(20); queue.enqueue(30); queue.enqueue(40); // queue contains [10, 20, 30, 40] // removes 10 document.write(queue.dequeue() + " dequeued from queue<br>"); // queue contains [20, 30, 40] // Front is now 20 document.write("Front item is " + queue.front() + "<br>"); // printing the rear element // Rear is 40 document.write("Rear item is " + queue.rear() + "<br>"); // This code is contributed by Susobhan Akhuli </script> |
| — |
Output
10 enqueued to queue
20 enqueued to queue
30 enqueued to queue
40 enqueued to queue
10 dequeued from queue
Front item is 20
Rear item is 40
Complexity Analysis:
- Time Complexity
| Operations | Complexity |
|---|---|
| Enqueue(insertion) | O(1) |
| Deque(deletion) | O(1) |
| Front(Get front) | O(1) |
| Rear(Get Rear) | O(1) |
| IsFull(Check queue is full or not) | O(1) |
| IsEmpty(Check queue is empty or not) | O(1) |
- Auxiliary Space:
O(N) where N is the size of the array for storing elements.
Advantages of Array Implementation:
- Easy to implement.
- A large amount of data can be managed efficiently with ease.
- Operations such as insertion and deletion can be performed with ease as it follows the first in first out rule.
Disadvantages of Array Implementation:
- Static Data Structure, fixed size.
- If the queue has a large number of enqueue and dequeue operations, at some point (in case of linear increment of front and rear indexes) we may not be able to insert elements in the queue even if the queue is empty (this problem is avoided by using circular queue).
- Maximum size of a queue must be defined prior.
Introduction to Queue - Data Structure and Algorithm Tutorials
Queue - Linked List Implementation
Queue – Linked List Implementation ==================================
In this article, the Linked List implementation of the queue data structure is discussed and implemented. Print ‘-1’ if the queue is empty.
Recommended Practice Implement Queue using Linked List
Approach: To solve the problem follow the below idea:
we maintain two pointers, front, and rear. The frontpoints to the first item of the queue andrearpoints to the last item.
- enQueue(): This operation adds a new node after the rearand moves the rearto the next node.
- deQueue(): This operation removes the front node and moves the frontto the next node.
Follow the below steps to solve the problem:
- Create a class QNode with data members integer data and QNode* next
- A parameterized constructor that takes an integer x value as a parameter and sets data equal to xand next as NULL
- Create a class Queue with data members QNode frontand rear
- Enqueue Operation with parameter x:
- Initialize QNode* tempwith data = x
- If the rear is set to NULL then set the front and rear to tempand return(Base Case)
- Else set rear next totemp and then move rear to temp
- Dequeue Operation:
- If the front is set to NULL return(Base Case)
- Initialize QNode tempwith front and set front to its next
- If the front is equal to NULLthen set the rear to NULL
- Delete temp from the memory
Below is the Implementation of the above approach:
C++
| // C++ program for the above approach #include <bits/stdc++.h> using namespace std; struct QNode { int data; QNode* next; QNode(int d) { data = d; next = NULL; } }; struct Queue { QNode *front, *rear; Queue() { front = rear = NULL; } void enQueue(int x) { // Create a new LL node QNode* temp = new QNode(x); // If queue is empty, then // new node is front and rear both if (rear == NULL) { front = rear = temp; return; } // Add the new node at // the end of queue and change rear rear->next = temp; rear = temp; } // Function to remove // a key from given queue q void deQueue() { // If queue is empty, return NULL. if (front == NULL) return; // Store previous front and // move front one node ahead QNode* temp = front; front = front->next; // If front becomes NULL, then // change rear also as NULL if (front == NULL) rear = NULL; delete (temp); } }; // Driver code int main() { Queue q; q.enQueue(10); q.enQueue(20); q.deQueue(); q.deQueue(); q.enQueue(30); q.enQueue(40); q.enQueue(50); q.deQueue(); cout << "Queue Front : " << ((q.front != NULL) ? (q.front)->data : -1)<< endl; cout << "Queue Rear : " << ((q.rear != NULL) ? (q.rear)->data : -1); } // This code is contributed by rathbhupendra |
| — |
C
| // A C program to demonstrate linked list based // implementation of queue #include <stdio.h> #include <stdlib.h> // A linked list (LL) node to store a queue entry struct QNode { int key; struct QNode* next; }; // The queue, front stores the front node of LL and rear // stores the last node of LL struct Queue { struct QNode *front, *rear; }; // A utility function to create a new linked list node. struct QNode* newNode(int k) { struct QNode* temp = (struct QNode*)malloc(sizeof(struct QNode)); temp->key = k; temp->next = NULL; return temp; } // A utility function to create an empty queue struct Queue* createQueue() { struct Queue* q = (struct Queue*)malloc(sizeof(struct Queue)); q->front = q->rear = NULL; return q; } // The function to add a key k to q void enQueue(struct Queue* q, int k) { // Create a new LL node struct QNode* temp = newNode(k); // If queue is empty, then new node is front and rear // both if (q->rear == NULL) { q->front = q->rear = temp; return; } // Add the new node at the end of queue and change rear q->rear->next = temp; q->rear = temp; } // Function to remove a key from given queue q void deQueue(struct Queue* q) { // If queue is empty, return NULL. if (q->front == NULL) return; // Store previous front and move front one node ahead struct QNode* temp = q->front; q->front = q->front->next; // If front becomes NULL, then change rear also as NULL if (q->front == NULL) q->rear = NULL; free(temp); } // Driver code int main() { struct Queue* q = createQueue(); enQueue(q, 10); enQueue(q, 20); deQueue(q); deQueue(q); enQueue(q, 30); enQueue(q, 40); enQueue(q, 50); deQueue(q); printf("Queue Front : %d \n", ((q->front != NULL) ? (q->front)->key : -1)); printf("Queue Rear : %d", ((q->rear != NULL) ? (q->rear)->key : -1)); return 0; } |
| — |
Java
| // Java program for linked-list implementation of queue // A linked list (LL) node to store a queue entry class QNode { int key; QNode next; // constructor to create a new linked list node public QNode(int key) { this.key = key; this.next = null; } } // A class to represent a queue // The queue, front stores the front node of LL and rear // stores the last node of LL class Queue { QNode front, rear; public Queue() { this.front = this.rear = null; } // Method to add an key to the queue. void enqueue(int key) { // Create a new LL node QNode temp = new QNode(key); // If queue is empty, then new node is front and // rear both if (this.rear == null) { this.front = this.rear = temp; return; } // Add the new node at the end of queue and change // rear this.rear.next = temp; this.rear = temp; } // Method to remove an key from queue. void dequeue() { // If queue is empty, return NULL. if (this.front == null) return; // Store previous front and move front one node // ahead QNode temp = this.front; this.front = this.front.next; // If front becomes NULL, then change rear also as // NULL if (this.front == null) this.rear = null; } } // Driver code public class Test { public static void main(String[] args) { Queue q = new Queue(); q.enqueue(10); q.enqueue(20); q.dequeue(); q.dequeue(); q.enqueue(30); q.enqueue(40); q.enqueue(50); q.dequeue(); System.out.println("Queue Front : " + ((q.front != null) ? (q.front).key : -1)); System.out.println("Queue Rear : " + ((q.rear != null) ? (q.rear).key : -1)); } } // This code is contributed by Gaurav Miglani |
| — |
Python3
| # Python3 program to demonstrate linked list # based implementation of queue # A linked list (LL) node # to store a queue entry class Node: def __init__(self, data): self.data = data self.next = None # A class to represent a queue # The queue, front stores the front node # of LL and rear stores the last node of LL class Queue: def __init__(self): self.front = self.rear = None def isEmpty(self): return self.front == None # Method to add an item to the queue def EnQueue(self, item): temp = Node(item) if self.rear == None: self.front = self.rear = temp return self.rear.next = temp self.rear = temp # Method to remove an item from queue def DeQueue(self): if self.isEmpty(): return temp = self.front self.front = temp.next if(self.front == None): self.rear = None # Driver Code if __name__ == '__main__': q = Queue() q.EnQueue(10) q.EnQueue(20) q.DeQueue() q.DeQueue() q.EnQueue(30) q.EnQueue(40) q.EnQueue(50) q.DeQueue() print("Queue Front : " + str(q.front.data if q.front != None else -1)) print("Queue Rear : " + str(q.rear.data if q.rear != None else -1)) |
| — |
C#
| // C# program for linked-list // implementation of queue using System; // A linked list (LL) node to // store a queue entry class QNode { public int key; public QNode next; // constructor to create // a new linked list node public QNode(int key) { this.key = key; this.next = null; } } // A class to represent a queue The queue, // front stores the front node of LL and // rear stores the last node of LL class Queue { public QNode front, rear; public Queue() { this.front = this.rear = null; } // Method to add an key to the queue. public void enqueue(int key) { // Create a new LL node QNode temp = new QNode(key); // If queue is empty, then new // node is front and rear both if (this.rear == null) { this.front = this.rear = temp; return; } // Add the new node at the // end of queue and change rear this.rear.next = temp; this.rear = temp; } // Method to remove an key from queue. public void dequeue() { // If queue is empty, return NULL. if (this.front == null) return; // Store previous front and // move front one node ahead this.front = this.front.next; // If front becomes NULL, // then change rear also as NULL if (this.front == null) this.rear = null; } } // Driver code public class Test { public static void Main(String[] args) { Queue q = new Queue(); q.enqueue(10); q.enqueue(20); q.dequeue(); q.dequeue(); q.enqueue(30); q.enqueue(40); q.enqueue(50); q.dequeue(); Console.WriteLine("Queue Front : " + ((q.front != null) ? (q.front).key : -1)); Console.WriteLine("Queue Rear : " + ((q.rear != null) ? (q.rear).key : -1)); } } // This code has been contributed by Rajput-Ji |
| — |
Javascript
| <script> // JavaScript program for linked-list implementation of queue class QNode { constructor(key) { this.key = key; this.next = null; } } let front = null, rear = null; function enqueue(key) { // Create a new LL node let temp = new QNode(key); // If queue is empty, then new node is front and rear both if (rear == null) { front = rear = temp; return; } // Add the new node at the end of queue and change rear rear.next = temp; rear = temp; } function dequeue() { // If queue is empty, return NULL. if (front == null) return; // Store previous front and move front one node ahead let temp = front; front = front.next; // If front becomes NULL, then change rear also as NULL if (front == null) rear = null; } enqueue(10); enqueue(20); dequeue(); dequeue(); enqueue(30); enqueue(40); enqueue(50); dequeue(); document.write("Queue Front : " + ((front != null) ? (front).key : -1) +"<br>"); document.write("Queue Rear : " + ((rear != null) ? (rear).key : -1) +"<br>"); // This code is contributed by avanitrachhadiya2155 </script> |
| — |
Output
Queue Front : 40
Queue Rear : 50
Time Complexity: O(1), The time complexity of both operations enqueue() and dequeue() is O(1) as it only changes a few pointers in both operations
Auxiliary Space: O(1), The auxiliary Space of both operations enqueue() and dequeue() is O(1) as constant extra space is required
Related Article:
Introduction and Array Implementation of Queue
Introduction and Array Implementation of Queue
Applications, Advantages and Disadvantages of Queue
Introduction to Circular Queue ==============================
What is a Circular Queue?
A Circular Queue is an extended version of a normal queue where the last element of the queue is connected to the first element of the queue forming a circle.
The operations are performed based on FIFO (First In First Out) principle. It is also called ‘Ring Buffer’.
In a normal Queue, we can insert elements until queue becomes full. But once queue becomes full, we can not insert the next element even if there is a space in front of queue.
Operations on Circular Queue:
- Front: Get the front item from the queue.
- Rear: Get the last item from the queue.
- enQueue(value) This function is used to insert an element into the circular queue. In a circular queue, the new element is always inserted at the rear position.
- Check whether the queue is full – [i.e., the rear end is in just before the front end in a circular manner].
- If it is full then display Queue is full.
- If the queue is not full then, insert an element at the end of the queue.
- deQueue() This function is used to delete an element from the circular queue. In a circular queue, the element is always deleted from the front position.
- Check whether the queue is Empty.
- If it is empty then display Queue is empty.
- If the queue is not empty, then get the last element and remove it from the queue.
Illustration of Circular Queue Operations:
Follow the below image for a better understanding of the enqueue and dequeue operations.
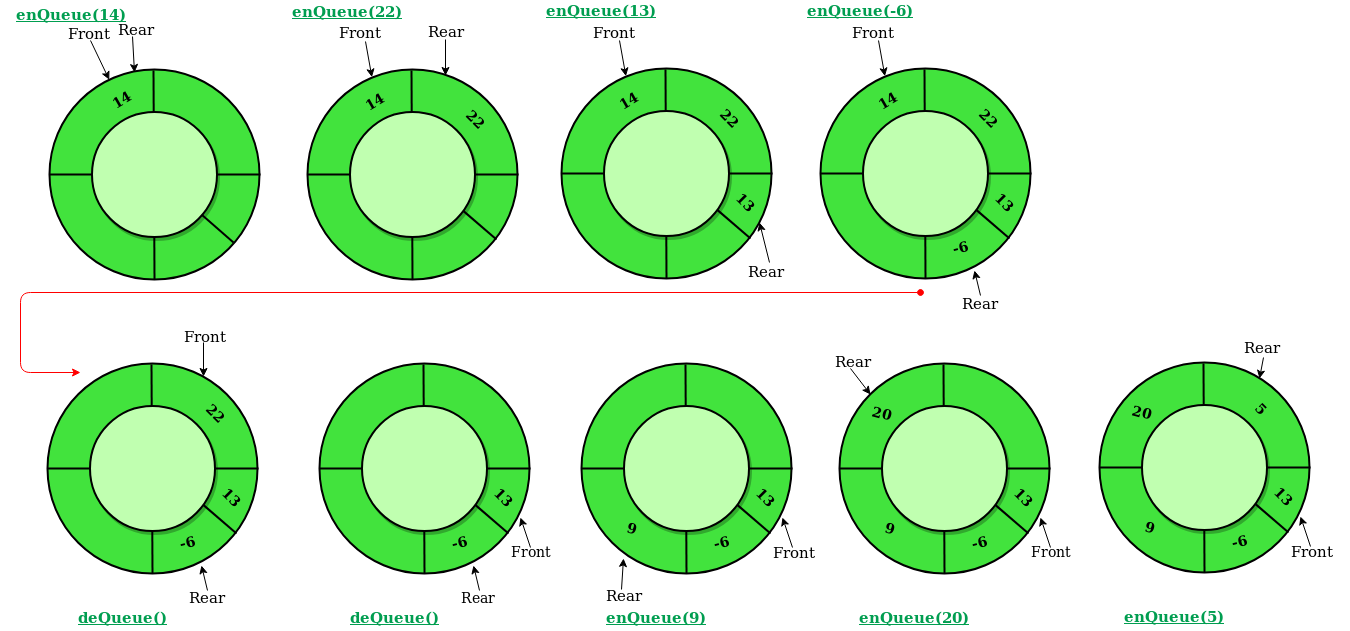 Working of Circular queue operations
Working of Circular queue operations
How to Implement a Circular Queue?
A circular queue can be implemented using two data structures:
Here we have shown the implementation of a circular queue using an array data structure.
Implement Circular Queue using Array:
- Initialize an array queue of size n, where n is the maximum number of elements that the queue can hold.
- Initialize two variables front and rear to -1.
- Enqueue: To enqueue an element x into the queue, do the following:
- Increment rear by 1.
- If rear is equal to n, set rear to 0.
- If front is -1, set front to 0.
- Set queue[rear] to x.
- Increment rear by 1.
- Dequeue: To dequeue an element from the queue, do the following:
- Check if the queue is empty by checking if front is -1.
- If it is, return an error message indicating that the queue is empty.
- Set x to queue[front].
- If front is equal to rear, set front and rear to -1.
- Otherwise, increment front by 1 and if front is equal to n, set front to 0.
- Return x.
- Check if the queue is empty by checking if front is -1.
Below is the implementation of the above idea:
C++
| // C or C++ program for insertion and // deletion in Circular Queue #include<bits/stdc++.h> using namespace std; class Queue { // Initialize front and rear int rear, front; // Circular Queue int size; int *arr; public: Queue(int s) { front = rear = -1; size = s; arr = new int[s]; } void enQueue(int value); int deQueue(); void displayQueue(); }; /* Function to create Circular queue */ void Queue::enQueue(int value) { if ((front == 0 && rear == size-1) || ((rear+1) % size == front)) { printf("\nQueue is Full"); return; } else if (front == -1) /* Insert First Element */ { front = rear = 0; arr[rear] = value; } else if (rear == size-1 && front != 0) { rear = 0; arr[rear] = value; } else { rear++; arr[rear] = value; } } // Function to delete element from Circular Queue int Queue::deQueue() { if (front == -1) { printf("\nQueue is Empty"); return INT_MIN; } int data = arr[front]; arr[front] = -1; if (front == rear) { front = -1; rear = -1; } else if (front == size-1) front = 0; else front++; return data; } // Function displaying the elements // of Circular Queue void Queue::displayQueue() { if (front == -1) { printf("\nQueue is Empty"); return; } printf("\nElements in Circular Queue are: "); if (rear >= front) { for (int i = front; i <= rear; i++) printf("%d ",arr[i]); } else { for (int i = front; i < size; i++) printf("%d ", arr[i]); for (int i = 0; i <= rear; i++) printf("%d ", arr[i]); } } /* Driver of the program */ int main() { Queue q(5); // Inserting elements in Circular Queue q.enQueue(14); q.enQueue(22); q.enQueue(13); q.enQueue(-6); // Display elements present in Circular Queue q.displayQueue(); // Deleting elements from Circular Queue printf("\nDeleted value = %d", q.deQueue()); printf("\nDeleted value = %d", q.deQueue()); q.displayQueue(); q.enQueue(9); q.enQueue(20); q.enQueue(5); q.displayQueue(); q.enQueue(20); return 0; } |
| — |
Java
| // Java program for insertion and // deletion in Circular Queue import java.util.ArrayList; class CircularQueue{ // Declaring the class variables. private int size, front, rear; // Declaring array list of integer type. private ArrayList<Integer> queue = new ArrayList<Integer>(); // Constructor CircularQueue(int size) { this.size = size; this.front = this.rear = -1; } // Method to insert a new element in the queue. public void enQueue(int data) { // Condition if queue is full. if((front == 0 && rear == size - 1) || (rear == (front - 1) % (size - 1))) { System.out.print("Queue is Full"); } // condition for empty queue. else if(front == -1) { front = 0; rear = 0; queue.add(rear, data); } else if(rear == size - 1 && front != 0) { rear = 0; queue.set(rear, data); } else { rear = (rear + 1); // Adding a new element if if(front <= rear) { queue.add(rear, data); } // Else updating old value else { queue.set(rear, data); } } } // Function to dequeue an element // form th queue. public int deQueue() { int temp; // Condition for empty queue. if(front == -1) { System.out.print("Queue is Empty"); // Return -1 in case of empty queue return -1; } temp = queue.get(front); // Condition for only one element if(front == rear) { front = -1; rear = -1; } else if(front == size - 1) { front = 0; } else { front = front + 1; } // Returns the dequeued element return temp; } // Method to display the elements of queue public void displayQueue() { // Condition for empty queue. if(front == -1) { System.out.print("Queue is Empty"); return; } // If rear has not crossed the max size // or queue rear is still greater then // front. System.out.print("Elements in the " + "circular queue are: "); if(rear >= front) { // Loop to print elements from // front to rear. for(int i = front; i <= rear; i++) { System.out.print(queue.get(i)); System.out.print(" "); } System.out.println(); } // If rear crossed the max index and // indexing has started in loop else { // Loop for printing elements from // front to max size or last index for(int i = front; i < size; i++) { System.out.print(queue.get(i)); System.out.print(" "); } // Loop for printing elements from // 0th index till rear position for(int i = 0; i <= rear; i++) { System.out.print(queue.get(i)); System.out.print(" "); } System.out.println(); } } // Driver code public static void main(String[] args) { // Initialising new object of // CircularQueue class. CircularQueue q = new CircularQueue(5); q.enQueue(14); q.enQueue(22); q.enQueue(13); q.enQueue(-6); q.displayQueue(); int x = q.deQueue(); // Checking for empty queue. if(x != -1) { System.out.print("Deleted value = "); System.out.println(x); } x = q.deQueue(); // Checking for empty queue. if(x != -1) { System.out.print("Deleted value = "); System.out.println(x); } q.displayQueue(); q.enQueue(9); q.enQueue(20); q.enQueue(5); q.displayQueue(); q.enQueue(20); } } // This code is contributed by Amit Mangal. |
| — |
C#
| // C# program for insertion and // deletion in Circular Queue using System; using System.Collections.Generic; public class CircularQueue{ // Declaring the class variables. private int size, front, rear; // Declaring array list of integer type. private List<int> queue = new List<int>(); // Constructor CircularQueue(int size) { this.size = size; this.front = this.rear = -1; } // Method to insert a new element in the queue. public void enQueue(int data) { // Condition if queue is full. if((front == 0 && rear == size - 1) || (rear == (front - 1) % (size - 1))) { Console.Write("Queue is Full"); } // condition for empty queue. else if(front == -1) { front = 0; rear = 0; queue.Add(data); } else if(rear == size - 1 && front != 0) { rear = 0; queue[rear]=data; } else { rear = (rear + 1); // Adding a new element if if(front <= rear) { queue.Add(data); } // Else updating old value else { queue[rear]=data; } } } // Function to dequeue an element // form th queue. public int deQueue() { int temp; // Condition for empty queue. if(front == -1) { Console.Write("Queue is Empty"); // Return -1 in case of empty queue return -1; } temp = queue[front]; // Condition for only one element if(front == rear) { front = -1; rear = -1; } else if(front == size - 1) { front = 0; } else { front = front + 1; } // Returns the dequeued element return temp; } // Method to display the elements of queue public void displayQueue() { // Condition for empty queue. if(front == -1) { Console.Write("Queue is Empty"); return; } // If rear has not crossed the max size // or queue rear is still greater then // front. Console.Write("Elements in the circular queue are: "); if(rear >= front) { // Loop to print elements from // front to rear. for(int i = front; i <= rear; i++) { Console.Write(queue[i]); Console.Write(" "); } Console.Write("\n"); } // If rear crossed the max index and // indexing has started in loop else { // Loop for printing elements from // front to max size or last index for(int i = front; i < size; i++) { Console.Write(queue[i]); Console.Write(" "); } // Loop for printing elements from // 0th index till rear position for(int i = 0; i <= rear; i++) { Console.Write(queue[i]); Console.Write(" "); } Console.Write("\n"); } } // Driver code static public void Main (){ // Initialising new object of // CircularQueue class. CircularQueue q = new CircularQueue(5); q.enQueue(14); q.enQueue(22); q.enQueue(13); q.enQueue(-6); q.displayQueue(); int x = q.deQueue(); // Checking for empty queue. if(x != -1) { Console.Write("Deleted value = "); Console.Write(x+"\n"); } x = q.deQueue(); // Checking for empty queue. if(x != -1) { Console.Write("Deleted value = "); Console.Write(x+"\n"); } q.displayQueue(); q.enQueue(9); q.enQueue(20); q.enQueue(5); q.displayQueue(); q.enQueue(20); } } // This code is contributed by shruti456rawal |
| — |
Python 3
| class CircularQueue(): # constructor def __init__(self, size): # initializing the class self.size = size # initializing queue with none self.queue = [None for i in range(size)] self.front = self.rear = -1 def enqueue(self, data): # condition if queue is full if ((self.rear + 1) % self.size == self.front): print(" Queue is Full\n") # condition for empty queue elif (self.front == -1): self.front = 0 self.rear = 0 self.queue[self.rear] = data else: # next position of rear self.rear = (self.rear + 1) % self.size self.queue[self.rear] = data def dequeue(self): if (self.front == -1): # condition for empty queue print ("Queue is Empty\n") # condition for only one element elif (self.front == self.rear): temp=self.queue[self.front] self.front = -1 self.rear = -1 return temp else: temp = self.queue[self.front] self.front = (self.front + 1) % self.size return temp def display(self): # condition for empty queue if(self.front == -1): print ("Queue is Empty") elif (self.rear >= self.front): print("Elements in the circular queue are:", end = " ") for i in range(self.front, self.rear + 1): print(self.queue[i], end = " ") print () else: print ("Elements in Circular Queue are:", end = " ") for i in range(self.front, self.size): print(self.queue[i], end = " ") for i in range(0, self.rear + 1): print(self.queue[i], end = " ") print () if ((self.rear + 1) % self.size == self.front): print("Queue is Full") # Driver Code ob = CircularQueue(5) ob.enqueue(14) ob.enqueue(22) ob.enqueue(13) ob.enqueue(-6) ob.display() print ("Deleted value = ", ob.dequeue()) print ("Deleted value = ", ob.dequeue()) ob.display() ob.enqueue(9) ob.enqueue(20) ob.enqueue(5) ob.display() # This code is contributed by AshwinGoel |
| — |
Javascript
| // JS program for insertion and // deletion in Circular Queue class Queue { constructor() { this.rear = -1; this.front = -1; this.size = 5; this.arr = new Array(); } enQueue(value) { if ((this.front == 0 && this.rear == this.size - 1) || (this.rear == (this.front - 1) % (this.size - 1))) { console.log("Queue is Full"); return; } else if (this.front == -1) /* Insert First Element */ { this.front = this.rear = 0; this.arr[this.rear] = value; } else if (this.rear == this.size - 1 && this.front != 0) { this.rear = 0; this.arr[this.rear] = value; } else { this.rear++; this.arr[this.rear] = value; } } deQueue() { if (this.front == -1) { console.log("Queue is Empty"); return INT_MIN; } let data = this.arr[this.front]; this.arr[this.front] = -1; if (this.front == this.rear) { this.front = -1; this.rear = -1; } else if (this.front == this.size - 1) this.front = 0; else this.front++; // console.log("Data: ",data); return data; } displayQueue() { if (this.front == -1) { console.log("Queue is Empty"); return; } console.log("\nElements in Circular Queue are: "); if (this.rear >= this.front) { for (let i = this.front; i <= this.rear; i++) console.log(this.arr[i]); } else { for (let i = this.front; i < this.size; i++) console.log(this.arr[i]); for (let i = 0; i <= this.rear; i++) console.log(this.arr[i]); } } } /* Driver of the program */ let q = new Queue; // Inserting elements in Circular Queue q.enQueue(14); q.enQueue(22); q.enQueue(13); q.enQueue(-6); // Display elements present in Circular Queue q.displayQueue(); // Deleting elements from Circular Queue console.log("Deleted value = ", q.deQueue()); console.log("Deleted value = ", q.deQueue()); q.displayQueue(); q.enQueue(9); q.enQueue(20); q.enQueue(5); q.displayQueue(); q.enQueue(20); // This code is contributed by ishankhandelwals. |
| — |
Output
Elements in Circular Queue are: 14 22 13 -6
Deleted value = 14
Deleted value = 22
Elements in Circular Queue are: 13 -6
Elements in Circular Queue are: 13 -6 9 20 5
Queue is Full
Complexity Analysis of Circular Queue Operations:
- Time Complexity:
- Enqueue: O(1) because no loop is involved for a single enqueue.
- Dequeue: O(1) because no loop is involved for one dequeue operation.
- Auxiliary Space: O(N) as the queue is of size N.
Applications of Circular Queue:
- Memory Management: The unused memory locations in the case of ordinary queues can be utilized in circular queues.
- Traffic system: In computer controlled traffic system, circular queues are used to switch on the traffic lights one by one repeatedly as per the time set.
- CPU Scheduling: Operating systems often maintain a queue of processes that are ready to execute or that are waiting for a particular event to occur.
What is Priority Queue | Introduction to Priority Queue =======================================================
A priority queue is a type of queue that arranges elements based on their priority values. Elements with higher priority values are typically retrieved before elements with lower priority values.
In a priority queue, each element has a priority value associated with it. When you add an element to the queue, it is inserted in a position based on its priority value. For example, if you add an element with a high priority value to a priority queue, it may be inserted near the front of the queue, while an element with a low priority value may be inserted near the back.
There are several ways to implement a priority queue, including using an array, linked list, heap, or binary search tree. Each method has its own advantages and disadvantages, and the best choice will depend on the specific needs of your application.
Priority queues are often used in real-time systems, where the order in which elements are processed can have significant consequences. They are also used in algorithms to improve their efficiencies, such as Dijkstra’s algorithm for finding the shortest path in a graph and the A* search algorithm for pathfinding.
Properties of Priority Queue
So, a priority Queue is an extension of the queue with the following properties.
- Every item has a priority associated with it.
- An element with high priority is dequeued before an element with low priority.
- If two elements have the same priority, they are served according to their order in the queue.
In the below priority queue, an element with a maximum ASCII value will have the highest priority. The elements with higher priority are served first.

How is Priority assigned to the elements in a Priority Queue?
In a priority queue, generally, the value of an element is considered for assigning the priority.
For example, the element with the highest value is assigned the highest priority and the element with the lowest value is assigned the lowest priority. The reverse case can also be used i.e., the element with the lowest value can be assigned the highest priority. Also, the priority can be assigned according to our needs.
Operations of a Priority Queue:
A typical priority queue supports the following operations:
1) Insertion in a Priority Queue
When a new element is inserted in a priority queue, it moves to the empty slot from top to bottom and left to right. However, if the element is not in the correct place then it will be compared with the parent node. If the element is not in the correct order, the elements are swapped. The swapping process continues until all the elements are placed in the correct position.
2) Deletion in a Priority Queue
As you know that in a max heap, the maximum element is the root node. And it will remove the element which has maximum priority first. Thus, you remove the root node from the queue. This removal creates an empty slot, which will be further filled with new insertion. Then, it compares the newly inserted element with all the elements inside the queue to maintain the heap invariant.
3) Peek in a Priority Queue
This operation helps to return the maximum element from Max Heap or the minimum element from Min Heap without deleting the node from the priority queue.
Types of Priority Queue:
1) Ascending Order Priority Queue
As the name suggests, in ascending order priority queue, the element with a lower priority value is given a higher priority in the priority list. For example, if we have the following elements in a priority queue arranged in ascending order like 4,6,8,9,10. Here, 4 is the smallest number, therefore, it will get the highest priority in a priority queue and so when we dequeue from this type of priority queue, 4 will remove from the queue and dequeue returns 4.
2) Descending order Priority Queue
The root node is the maximum element in a max heap, as you may know. It will also remove the element with the highest priority first. As a result, the root node is removed from the queue. This deletion leaves an empty space, which will be filled with fresh insertions in the future. The heap invariant is then maintained by comparing the newly inserted element to all other entries in the queue.
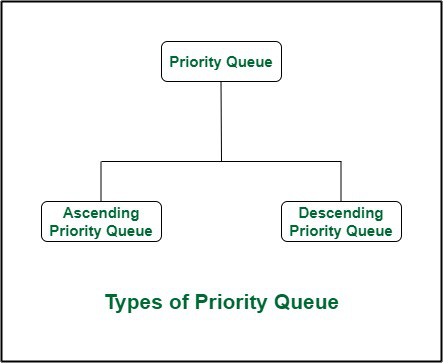 Types of Priority Queues
Types of Priority Queues
Difference between Priority Queue and Normal Queue?
There is no priority attached to elements in a queue, the rule of first-in-first-out(FIFO) is implemented whereas, in a priority queue, the elements have a priority. The elements with higher priority are served first.
How to Implement Priority Queue?
Priority queue can be implemented using the following data structures:
- Arrays
- Linked list
- Heap data structure
- Binary search tree
Let’s discuss all these in detail.
1) Implement Priority Queue Using Array:
A simple implementation is to use an array of the following structure.
struct item {
int item;
int priority;
}
- enqueue(): This function is used to insert new data into the queue.
- dequeue(): This function removes the element with the highest priority from the queue.
- peek()/top(): This function is used to get the highest priority element in the queue without removing it from the queue.
| Arrays | enqueue() | dequeue() | peek() |
|---|---|---|---|
| Time Complexity | O(1) | O(n) | O(n) |
C++
| // C++ program to implement Priority Queue // using Arrays #include <bits/stdc++.h> using namespace std; // Structure for the elements in the // priority queue struct item { int value; int priority; }; // Store the element of a priority queue item pr[100000]; // Pointer to the last index int size = -1; // Function to insert a new element // into priority queue void enqueue(int value, int priority) { // Increase the size size++; // Insert the element pr[size].value = value; pr[size].priority = priority; } // Function to check the top element int peek() { int highestPriority = INT_MIN; int ind = -1; // Check for the element with // highest priority for (int i = 0; i <= size; i++) { // If priority is same choose // the element with the // highest value if (highestPriority == pr[i].priority && ind > -1 && pr[ind].value < pr[i].value) { highestPriority = pr[i].priority; ind = i; } else if (highestPriority < pr[i].priority) { highestPriority = pr[i].priority; ind = i; } } // Return position of the element return ind; } // Function to remove the element with // the highest priority void dequeue() { // Find the position of the element // with highest priority int ind = peek(); // Shift the element one index before // from the position of the element // with highest priority is found for (int i = ind; i < size; i++) { pr[i] = pr[i + 1]; } // Decrease the size of the // priority queue by one size--; } // Driver Code int main() { // Function Call to insert elements // as per the priority enqueue(10, 2); enqueue(14, 4); enqueue(16, 4); enqueue(12, 3); // Stores the top element // at the moment int ind = peek(); cout << pr[ind].value << endl; // Dequeue the top element dequeue(); // Check the top element ind = peek(); cout << pr[ind].value << endl; // Dequeue the top element dequeue(); // Check the top element ind = peek(); cout << pr[ind].value << endl; return 0; } |
| — |
Java
| // Java program to implement Priority Queue // using Arrays import java.util.*; // Structure for the elements in the // priority queue class item { public int value; public int priority; }; class GFG { // Store the element of a priority queue static item[] pr = new item[100000]; // Pointer to the last index static int size = -1; // Function to insert a new element // into priority queue static void enqueue(int value, int priority) { // Increase the size size++; // Insert the element pr[size] = new item(); pr[size].value = value; pr[size].priority = priority; } // Function to check the top element static int peek() { int highestPriority = Integer.MIN_VALUE; int ind = -1; // Check for the element with // highest priority for (int i = 0; i <= size; i++) { // If priority is same choose // the element with the // highest value if (highestPriority == pr[i].priority && ind > -1 && pr[ind].value < pr[i].value) { highestPriority = pr[i].priority; ind = i; } else if (highestPriority < pr[i].priority) { highestPriority = pr[i].priority; ind = i; } } // Return position of the element return ind; } // Function to remove the element with // the highest priority static void dequeue() { // Find the position of the element // with highest priority int ind = peek(); // Shift the element one index before // from the position of the element // with highest priority is found for (int i = ind; i < size; i++) { pr[i] = pr[i + 1]; } // Decrease the size of the // priority queue by one size--; } public static void main(String[] args) { // Function Call to insert elements // as per the priority enqueue(10, 2); enqueue(14, 4); enqueue(16, 4); enqueue(12, 3); // Stores the top element // at the moment int ind = peek(); System.out.println(pr[ind].value); // Dequeue the top element dequeue(); // Check the top element ind = peek(); System.out.println(pr[ind].value); // Dequeue the top element dequeue(); // Check the top element ind = peek(); System.out.println(pr[ind].value); } } // this code is contributed by phasing17 |
| — |
Python3
| import sys # Structure for the elements in the # priority queue class item : value = 0 priority = 0 class GFG : # Store the element of a priority queue pr = [None] * (100000) # Pointer to the last index size = -1 # Function to insert a new element # into priority queue @staticmethod def enqueue( value, priority) : # Increase the size GFG.size += 1 # Insert the element GFG.pr[GFG.size] = item() GFG.pr[GFG.size].value = value GFG.pr[GFG.size].priority = priority # Function to check the top element @staticmethod def peek() : highestPriority = -sys.maxsize ind = -1 # Check for the element with # highest priority i = 0 while (i <= GFG.size) : # If priority is same choose # the element with the # highest value if (highestPriority == GFG.pr[i].priority and ind > -1 and GFG.pr[ind].value < GFG.pr[i].value) : highestPriority = GFG.pr[i].priority ind = i elif(highestPriority < GFG.pr[i].priority) : highestPriority = GFG.pr[i].priority ind = i i += 1 # Return position of the element return ind # Function to remove the element with # the highest priority @staticmethod def dequeue() : # Find the position of the element # with highest priority ind = GFG.peek() # Shift the element one index before # from the position of the element # with highest priority is found i = ind while (i < GFG.size) : GFG.pr[i] = GFG.pr[i + 1] i += 1 # Decrease the size of the # priority queue by one GFG.size -= 1 @staticmethod def main( args) : # Function Call to insert elements # as per the priority GFG.enqueue(10, 2) GFG.enqueue(14, 4) GFG.enqueue(16, 4) GFG.enqueue(12, 3) # Stores the top element # at the moment ind = GFG.peek() print(GFG.pr[ind].value) # Dequeue the top element GFG.dequeue() # Check the top element ind = GFG.peek() print(GFG.pr[ind].value) # Dequeue the top element GFG.dequeue() # Check the top element ind = GFG.peek() print(GFG.pr[ind].value) if __name__=="__main__": GFG.main([]) # This code is contributed by aadityaburujwale. |
| — |
C#
| // C# program to implement Priority Queue // using Arrays using System; // Structure for the elements in the // priority queue public class item { public int value; public int priority; }; public class GFG { // Store the element of a priority queue static item[] pr = new item[100000]; // Pointer to the last index static int size = -1; // Function to insert a new element // into priority queue static void enqueue(int value, int priority) { // Increase the size size++; // Insert the element pr[size] = new item(); pr[size].value = value; pr[size].priority = priority; } // Function to check the top element static int peek() { int highestPriority = int.MinValue; int ind = -1; // Check for the element with // highest priority for (int i = 0; i <= size; i++) { // If priority is same choose // the element with the // highest value if (highestPriority == pr[i].priority && ind > -1 && pr[ind].value < pr[i].value) { highestPriority = pr[i].priority; ind = i; } else if (highestPriority < pr[i].priority) { highestPriority = pr[i].priority; ind = i; } } // Return position of the element return ind; } // Function to remove the element with // the highest priority static void dequeue() { // Find the position of the element // with highest priority int ind = peek(); // Shift the element one index before // from the position of the element // with highest priority is found for (int i = ind; i < size; i++) { pr[i] = pr[i + 1]; } // Decrease the size of the // priority queue by one size--; } public static void Main(string[] args) { // Function Call to insert elements // as per the priority enqueue(10, 2); enqueue(14, 4); enqueue(16, 4); enqueue(12, 3); // Stores the top element // at the moment int ind = peek(); Console.WriteLine(pr[ind].value); // Dequeue the top element dequeue(); // Check the top element ind = peek(); Console.WriteLine(pr[ind].value); // Dequeue the top element dequeue(); // Check the top element ind = peek(); Console.WriteLine(pr[ind].value); } } //this code is contributed by phasing17 |
| — |
Javascript
| // JavaScript program to implement Priority Queue // using Arrays // Structure for the elements in the // priority queue class item { constructor() { this.value; this.priority; } }; // Store the element of a priority queue let pr = []; for (var i = 0; i < 100000; i++) pr.push(new item()); // Pointer to the last index let size = -1; // Function to insert a new element // into priority queue function enqueue(value, priority) { // Increase the size size++; // Insert the element pr[size] = new item(); pr[size].value = value; pr[size].priority = priority; } // Function to check the top element function peek() { let highestPriority = Number.MIN_SAFE_INTEGER; let ind = -1; // Check for the element with // highest priority for (var i = 0; i <= size; i++) { // If priority is same choose // the element with the // highest value if (highestPriority == pr[i].priority && ind > -1 && pr[ind].value < pr[i].value) { highestPriority = pr[i].priority; ind = i; } else if (highestPriority < pr[i].priority) { highestPriority = pr[i].priority; ind = i; } } // Return position of the element return ind; } // Function to remove the element with // the highest priority function dequeue() { // Find the position of the element // with highest priority let ind = peek(); // Shift the element one index before // from the position of the element // with highest priority is found for (var i = ind; i < size; i++) { pr[i] = pr[i + 1]; } // Decrease the size of the // priority queue by one size--; } // Function Call to insert elements // as per the priority enqueue(10, 2); enqueue(14, 4); enqueue(16, 4); enqueue(12, 3); // Stores the top element // at the moment let ind = peek(); console.log(pr[ind].value); // Dequeue the top element dequeue(); // Check the top element ind = peek(); console.log(pr[ind].value); // Dequeue the top element dequeue(); // Check the top element ind = peek(); console.log(pr[ind].value); // this code is contributed by phasing17 |
| — |
Output
16
14
12
Note: Read this articlefor more details.
2) Implement Priority Queue Using Linked List:
In a LinkedList implementation, the entries are sorted in descending order based on their priority. The highest priority element is always added to the front of the priority queue, which is formed using linked lists. The functions like push(), pop(), and peek() are used to implement a priority queue using a linked list and are explained as follows:
- push(): This function is used to insert new data into the queue.
- pop(): This function removes the element with the highest priority from the queue.
- peek() / top(): This function is used to get the highest priority element in the queue without removing it from the queue.
| Linked List | push() | pop() | peek() |
|---|---|---|---|
| Time Complexity | O(n) | O(1) | O(1) |
C++
| // C++ code to implement Priority Queue // using Linked List #include <bits/stdc++.h> using namespace std; // Node typedef struct node { int data; // Lower values indicate // higher priority int priority; struct node* next; } Node; // Function to create a new node Node* newNode(int d, int p) { Node* temp = (Node*)malloc(sizeof(Node)); temp->data = d; temp->priority = p; temp->next = NULL; return temp; } // Return the value at head int peek(Node** head) { return (*head)->data; } // Removes the element with the // highest priority form the list void pop(Node** head) { Node* temp = *head; (*head) = (*head)->next; free(temp); } // Function to push according to priority void push(Node** head, int d, int p) { Node* start = (*head); // Create new Node Node* temp = newNode(d, p); // Special Case: The head of list has // lesser priority than new node if ((*head)->priority < p) { // Insert New Node before head temp->next = *head; (*head) = temp; } else { // Traverse the list and find a // position to insert new node while (start->next != NULL && start->next->priority > p) { start = start->next; } // Either at the ends of the list // or at required position temp->next = start->next; start->next = temp; } } // Function to check is list is empty int isEmpty(Node** head) { return (*head) == NULL; } // Driver code int main() { // Create a Priority Queue // 7->4->5->6 Node* pq = newNode(4, 1); push(&pq, 5, 2); push(&pq, 6, 3); push(&pq, 7, 0); while (!isEmpty(&pq)) { cout << " " << peek(&pq); pop(&pq); } return 0; } |
| — |
Java
| // Java code to implement Priority Queue // using Linked List import java.util.* ; class Solution { // Node static class Node { int data; // Lower values indicate higher priority int priority; Node next; } static Node node = new Node(); // Function to Create A New Node static Node newNode(int d, int p) { Node temp = new Node(); temp.data = d; temp.priority = p; temp.next = null; return temp; } // Return the value at head static int peek(Node head) { return (head).data; } // Removes the element with the // highest priority from the list static Node pop(Node head) { Node temp = head; (head) = (head).next; return head; } // Function to push according to priority static Node push(Node head, int d, int p) { Node start = (head); // Create new Node Node temp = newNode(d, p); // Special Case: The head of list has lesser // priority than new node. So insert new // node before head node and change head node. if ((head).priority < p) { // Insert New Node before head temp.next = head; (head) = temp; } else { // Traverse the list and find a // position to insert new node while (start.next != null && start.next.priority > p) { start = start.next; } // Either at the ends of the list // or at required position temp.next = start.next; start.next = temp; } return head; } // Function to check is list is empty static int isEmpty(Node head) { return ((head) == null)?1:0; } // Driver code public static void main(String args[]) { // Create a Priority Queue // 7.4.5.6 Node pq = newNode(4, 1); pq =push(pq, 5, 2); pq =push(pq, 6, 3); pq =push(pq, 7, 0); while (isEmpty(pq)==0) { System.out.printf("%d ", peek(pq)); pq=pop(pq); } } } // This code is contributed by ishankhandelwals. |
| — |
Python
| # Python3 code to implement Priority Queue # using Singly Linked List # Class to create new node which includes # Node Data, and Node Priority class PriorityQueueNode: def _init_(self, value, pr): self.data = value self.priority = pr self.next = None # Implementation of Priority Queue class PriorityQueue: def _init_(self): self.front = None # Method to check Priority Queue is Empty # or not if Empty then it will return True # Otherwise False def isEmpty(self): return True if self.front == None else False # Method to add items in Priority Queue # According to their priority value def push(self, value, priority): # Condition check for checking Priority # Queue is empty or not if self.isEmpty() == True: # Creating a new node and assigning # it to class variable self.front = PriorityQueueNode(value, priority) # Returning 1 for successful execution return 1 else: # Special condition check to see that # first node priority value if self.front.priority < priority: # Creating a new node newNode = PriorityQueueNode(value, priority) # Updating the new node next value newNode.next = self.front # Assigning it to self.front self.front = newNode # Returning 1 for successful execution return 1 else: # Traversing through Queue until it # finds the next smaller priority node temp = self.front while temp.next: # If same priority node found then current # node will come after previous node if priority >= temp.next.priority: break temp = temp.next newNode = PriorityQueueNode(value, priority) newNode.next = temp.next temp.next = newNode # Returning 1 for successful execution return 1 # Method to remove high priority item # from the Priority Queue def pop(self): # Condition check for checking # Priority Queue is empty or not if self.isEmpty() == True: return else: # Removing high priority node from # Priority Queue, and updating front # with next node self.front = self.front.next return 1 # Method to return high priority node # value Not removing it def peek(self): # Condition check for checking Priority # Queue is empty or not if self.isEmpty() == True: return else: return self.front.data # Method to Traverse through Priority # Queue def traverse(self): # Condition check for checking Priority # Queue is empty or not if self.isEmpty() == True: return "Queue is Empty!" else: temp = self.front while temp: print(temp.data, end=" ") temp = temp.next # Driver code if _name_ == "_main_": # Creating an instance of Priority # Queue, and adding values # 7 -> 4 -> 5 -> 6 pq = PriorityQueue() pq.push(4, 1) pq.push(5, 2) pq.push(6, 3) pq.push(7, 0) # Traversing through Priority Queue pq.traverse() # Removing highest Priority item # for priority queue pq.pop() |
| — |
C#
| // C# code to implement Priority Queue // using Linked List using System; class GFG { // Node public class Node { public int data; // Lower values indicate // higher priority public int priority; public Node next; } public static Node node = new Node(); // Function to Create A New Node public static Node newNode(int d, int p) { Node temp = new Node(); temp.data = d; temp.priority = p; temp.next = null; return temp; } // Return the value at head public static int peek(Node head) { return (head).data; } // Removes the element with the // highest priority from the list public static Node pop(Node head) { Node temp = head; (head) = (head).next; return head; } // Function to push according to priority public static Node push(Node head, int d, int p) { Node start = (head); // Create new Node Node temp = newNode(d, p); // Special Case: The head of list // has lesser priority than new node. // So insert new node before head node // and change head node. if ((head).priority < p) { // Insert New Node before head temp.next = head; (head) = temp; } else { // Traverse the list and find a // position to insert new node while (start.next != null && start.next.priority > p) { start = start.next; } // Either at the ends of the list // or at required position temp.next = start.next; start.next = temp; } return head; } // Function to check is list is empty public static int isEmpty(Node head) { return ((head) == null) ? 1 : 0; } // Driver code public static void Main(string[] args) { // Create a Priority Queue // 7.4.5.6 Node pq = newNode(4, 1); pq = push(pq, 5, 2); pq = push(pq, 6, 3); pq = push(pq, 7, 0); while (isEmpty(pq) == 0) { Console.Write("{0:D} ", peek(pq)); pq = pop(pq); } } } // This code is contributed by ishankhandelwals. |
| — |
Javascript
| // JavaScript code to implement Priority Queue // using Linked List // Node class Node { // Lower values indicate // higher priority constructor() { this.data = 0; this.priority = 0; this.next = null; } } var node = new Node(); // Function to Create A New Node function newNode(d, p) { var temp = new Node(); temp.data = d; temp.priority = p; temp.next = null; return temp; } // Return the value at head function peek(head) { return head.data; } // Removes the element with the // highest priority from the list function pop(head) { var temp = head; head = head.next; return head; } // Function to push according to priority function push(head, d, p) { var start = head; // Create new Node var temp = newNode(d, p); // Special Case: The head of list // has lesser priority than new node. // So insert new node before head node // and change head node. if (head.priority < p) { // Insert New Node before head temp.next = head; head = temp; } else { // Traverse the list and find a // position to insert new node while (start.next != null && start.next.priority > p) { start = start.next; } // Either at the ends of the list // or at required position temp.next = start.next; start.next = temp; } return head; } // Function to check is list is empty function isEmpty(head) { return head == null ? 1 : 0; } // Driver code // Create a Priority Queue // 7.4.5.6 var pq = newNode(4, 1); pq = push(pq, 5, 2); pq = push(pq, 6, 3); pq = push(pq, 7, 0); while (isEmpty(pq) == 0) { console.log(peek(pq)," "); pq = pop(pq); } // This code is contributed by ishankhandelwals. |
| — |
Output
6 5 4 7
Refer to this article for more details.
Note: We can also use Linked List, time complexity of all operations with linked list remains same as array. The advantage with linked list isdeleteHighestPriority()can be more efficient as we don’t have to move items.
3) Implement Priority Queue Using Heaps:
Binary Heap is generally preferred for priority queue implementation because heaps provide better performance compared to arrays or LinkedList. Considering the properties of a heap, The entry with the largest key is on the top and can be removed immediately. It will, however, take time O(log n) to restore the heap property for the remaining keys. However if another entry is to be inserted immediately, then some of this time may be combined with the O(log n) time needed to insert the new entry. Thus the representation of a priority queue as a heap proves advantageous for large n, since it is represented efficiently in contiguous storage and is guaranteed to require only logarithmic time for both insertions and deletions. Operations on Binary Heap are as follows:
- insert(p): Inserts a new element with priority p.
- extractMax(): Extracts an element with maximum priority.
- remove(i): Removes an element pointed by an iterator i.
- getMax(): Returns an element with maximum priority.
- changePriority(i, p): Changes the priority of an element pointed by i to p.
| Binary Heap | insert() | remove() | peek() |
|---|---|---|---|
| Time Complexity | O(log n) | O(log n) | O(1) |
Refer to this article for code implementation.
4) Implement Priority Queue Using Binary Search Tree:
A Self-Balancing Binary Search Tree like AVL Tree, Red-Black Tree, etc. can also be used to implement a priority queue. Operations like peek(), insert() and delete() can be performed using BST.
| Binary Search Tree | peek() | insert() | delete() |
|---|---|---|---|
| Time Complexity | O(1) | O(log n) | O(log n) |
Applications of Priority Queue:
- CPU Scheduling
- Graph algorithms like Dijkstra’s shortest path algorithm, Prim’s Minimum Spanning Tree, etc.
- Stack Implementation
- All queue applications where priority is involved.
- Data compression in Huffman code
- Event-driven simulation such as customers waiting in a queue.
- Finding Kth largest/smallest element.
Advantages of Priority Queue:
- It helps to access the elements in a faster way. This is because elements in a priority queue are ordered by priority, one can easily retrieve the highest priority element without having to search through the entire queue.
- The ordering of elements in a Priority Queue is done dynamically. Elements in a priority queue can have their priority values updated, which allows the queue to dynamically reorder itself as priorities change.
- Efficient algorithms can be implemented. Priority queues are used in many algorithms to improve their efficiency, such as Dijkstra’s algorithm for finding the shortest path in a graph and the A* search algorithm for pathfinding.
- Included in real-time systems. This is because priority queues allow you to quickly retrieve the highest priority element, they are often used in real-time systems where time is of the essence.
Disadvantages of Priority Queue:
- High complexity. Priority queues are more complex than simple data structures like arrays and linked lists, and may be more difficult to implement and maintain.
- High consumption of memory. Storing the priority value for each element in a priority queue can take up additional memory, which may be a concern in systems with limited resources.
- It is not always the most efficient data structure. In some cases, other data structures like heaps or binary search trees may be more efficient for certain operations, such as finding the minimum or maximum element in the queue.
- At times it is less predictable:. This is because the order of elements in a priority queue is determined by their priority values, the order in which elements are retrieved may be less predictable than with other data structures like stacks or queues, which follow a first-in, first-out (FIFO) or last-in, first-out (LIFO) order.
See also:
- Applications of Priority Queue
- Priority Queue in C++
- Priority Queue in Java
- Priority Queue in Python
- Priority Queue in JavaScript
- Recent articles on Priority Queue!
Why can’t a Priority Queue wrap around like an ordinary Queue?
Deque | Set 1 (Introduction and Applications) =============================================
Deque or Double Ended Queue is a generalized version of Queue data structure that allows insert and delete at both ends.
Operations on Deque: Below is a table showing some basic operations along with their time complexity, performed on deques.
| Operation | Description | Time Complexity |
|---|---|---|
| push_front() | Inserts the element at the beginning. | O(1) |
| push_back() | Adds element at the end. | O(1) |
| pop_front() | Removes the first element from the deque. | O(1) |
| pop_back() | Removes the last element from the deque. | O(1) |
| front() | Gets the front element from the deque. | O(1) |
| back() | Gets the last element from the deque. | O(1) |
| empty() | Checks whether the deque is empty or not. | O(1) |
| size() | Determines the number of elements in the deque. | O(1) |
Other operations performed on deques are explained as follows:
clear(): Remove all the elements from the deque. It leaves the deque with a size of 0.
erase(): Remove one or more elements from the deque. It takes an iterator specifying the position of the first element to be removed, and an optional second iterator specifying the position of the last element to be removed.
swap(): Swap the contents of one deque with another deque.
emplace_front(): Insert a new element at the front of the deque. It is similar to the insert operation, but it avoids the copy constructor of the element being inserted.
emplace_back(): Insert a new element at the back of the deque. It is similar to the insert operation, but it avoids the copy constructor of the element being inserted.
resize(): Change the number of elements in the deque to a specific number. If the new size is larger than the current size, new elements are appended to the deque. If the new size is smaller than the current size, elements are removed from the deque.
assign(): Assign new values to the elements in the deque. It replaces the current contents of the deque with new elements.
reverse(): Reverse the order of the elements in the deque.
sort(): Sort the elements in the deque in ascending order. It uses the less-than operator to compare the elements.
Applications of Deque: Since Deque supports both stack and queue operations, it can be used as both. The Deque data structure supports clockwise and anticlockwise rotations in O(1) time which can be useful in certain applications. Also, the problems where elements need to be removed and or added to both ends can be efficiently solved using Deque. For example see the Maximum of all subarrays of size k problem., 0-1 BFS, and Find the first circular tour that visits all petrol pumps. See the wiki page for another example of the A-Steal job scheduling algorithm where Deque is used as deletions operation is required at both ends.
Some Practical Applications of Deque:
- Applied as both stack and queue, as it supports both operations.
- Storing a web browser’s history.
- Storing a software application’s list of undo operations.
- Job scheduling algorithm
Monotonic Deque :
- It is deque which stores elements in strictly increasing order or in strictly decreasing order
- To maintain monotonicity, we need to delete elements
- For example – Consider monotonic(decreasing) deque dq = {5, 4, 2, 1}
- Insert 3 into dq
- So we need to delete elements till dq.back() < 3 to insert 3 into dq (2,1 are the deleted elements)
- Resulting dq = {5, 4, 3}
- Applications of monotonic deque :
- It can be used to get next maximum in a subarray (sliding-window-maximum-of-all-subarrays-of-size-k) by using monotonically decreasing deque
- Like this it can be used to get previous maximum also in a subarray
- It is frequentlyused in sliding window problems (hard)
Other Applications:
Deques have several other applications, some of which include:
- Palindrome checking: Deques can be used to check if a word or phrase is a palindrome. By inserting each character of the word or phrase into a deque, it is possible to check if the word or phrase is a palindrome by comparing the first and last characters, the second and second-to-last characters, and so on.
- Graph traversal: Deques can be used to implement Breadth-First Search (BFS) on a graph. BFS uses a queue to keep track of the vertices to be visited next, and a deque can be used as an alternative to a queue in this case.
- Task scheduler: Deques can be used to implement a task scheduler that keeps track of tasks to be executed. Tasks can be added to the back of the deque, and the scheduler can remove tasks from the front of the deque and execute them.
- Multi-level undo/redo functionality: Deques can be used to implement undo and redo functionality in applications. Each time a user performs an action, the current state of the application is pushed onto the deque. When the user undoes an action, the front of the deque is popped, and the previous state is restored. When the user redoes an action, the next state is popped from the deque.
- In computer science, deque can be used in many algorithms like LRU Cache, Round Robin Scheduling, Expression Evaluation.
Language Support: C++ STL provides an implementation of Deque as std::deque and Java provides the Deque interface. See this for more details. Deque in Java Deque in Python
Implementation: A Deque can be implemented either using a doubly-linked list or a circular array. In both implementations, we can implement all operations in O(1) time. We will soon be discussing the C/C++ implementation of the Deque Data structure. Implementation of Deque using circular arrayPlease write comments if you find the above codes/algorithms incorrect, or find other ways to solve the same problem.
Applications, Advantages and Disadvantages of Deque